
【题目】数学课上,同学们遇到这样一个问题:
如图1,已知![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 与
与 ![]() 的角平分线,请同学们根据题中的条件提出问题,大家一起来解决(本题出现的角均小于平角)
的角平分线,请同学们根据题中的条件提出问题,大家一起来解决(本题出现的角均小于平角)
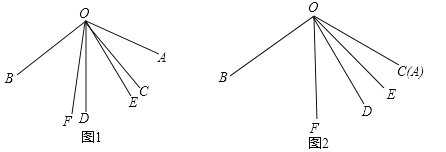
同学们经过思考后,交流了自己的想法:
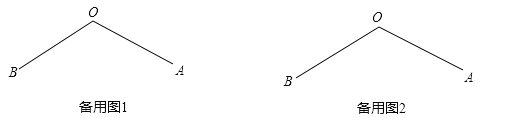
小强说:“如图2,若![]() 与
与![]() 重合,且
重合,且![]() ,
,![]() 时,可求
时,可求![]() 的度数.”
的度数.”
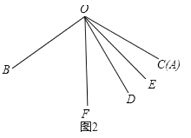
小伟说:“在小强提出问題的前提条件下,将![]() 的
的![]() 边从
边从![]() 边开始绕点
边开始绕点![]() 逆时针
逆时针
转动![]() ,可求出
,可求出![]() 的值.”
的值.”
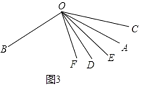
老师说:“在原題的条件下,借助射线![]() 的不同位置可得出的数量关系.”
的不同位置可得出的数量关系.”
(1)请解决小强提出的问题;
(2)在备用图1中,补充完整的图形,并解决小伟提出的问题
(3)在备用图2中,补充完整的图形,并解决老师提出的问题,即求![]() 三者之间的的数量关系.
三者之间的的数量关系.
【答案】(1)45![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
![]() 、
、![]()
![]() 、180
、180![]()
![]()
![]() 、180
、180![]()
![]()
![]() .
.
【解析】
(1)根据角平分线定义即可解决小强提出的问题;
(2)在备用图1中,补充完整的图形,根据角平分线定义及角的和差计算即可解决小伟提出的问题;
(3)在备用图2中,补充完整的图形,分四种情况讨论即可解决老师提出的问题,进而求出![]() 三者之间的数量关系.
三者之间的数量关系.
(1)如图2,
∵∠AOB=120![]() ,OF是∠BOC的角平分线
,OF是∠BOC的角平分线
∴∠FOC=![]() ∠AOB=60
∠AOB=60![]()
∵∠COD=30![]() ,OE是∠AOD的角平分线
,OE是∠AOD的角平分线
∴∠EOC=![]() ∠COD=15
∠COD=15![]()
∴∠EOF=∠FOC∠EOC=45![]()
答:∠EOF的度数为45![]() ;
;
(2)如图3,
∵OE、OF分别是∠AOD与∠BOC的角平分线,
∴设∠AO=∠DOE=![]() ∠AOD=
∠AOD=![]()
∠BOF=∠COF=![]() ∠BOC=
∠BOC=![]()
∴∠BOE=∠AOB∠AOE=120![]()
![]()
∵∠BOC=∠AOB+∠COD∠AOD=150![]() 2
2![]()
∴∠COF=75![]()
![]()
∴∠DOF=∠COF∠COD=75![]()
![]() 30
30![]() =45°
=45°![]()
∴∠BOE∠DOF=(120![]()
![]() )((45
)((45![]()
![]() )=75
)=75![]()
∵∠COE=∠COD∠DOE=30![]()
![]()
∴∠EOF=∠FOC∠COE=(75![]() )(30
)(30![]()
![]() )=45
)=45![]()
∴![]() =
=![]()
答:![]() 的值为
的值为![]() ;
;
(3)∵OE、OF分别是∠AOD与∠BOC的角平分线,
∴设∠AOE=∠DOE=![]() ∠AOD=
∠AOD=![]()
∠BOF=∠COF=![]() ∠BOC
∠BOC
∴①如图4,
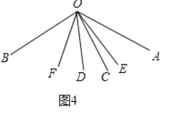
∠AOC=∠AOD∠COD=2![]() β
β
∵∠BOC=∠AOB∠AOC
=![]() (2
(2![]()
![]() )
)
=![]() 2
2![]() +
+![]()
∴∠FOC=![]() ∠BOC=
∠BOC=![]()
![]()
![]() +
+![]()
![]()
∵∠COE=∠DOE∠COD=![]()
![]()
∴∠EOF=∠FOC+∠COE
=![]()
![]()
![]() +
+![]()
![]() +
+![]()
![]()
=![]() (
(![]()
![]() ).
).
②如图5,
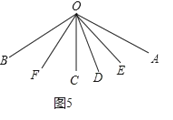
∠AOC=∠AOD+∠COD=2![]() +
+![]()
∵∠BOC=∠AOB∠AOC
=![]() (2
(2![]() +
+![]() )
)
=![]() 2
2![]()
![]()
∴∠FOC=![]() ∠BOC=
∠BOC=![]()
![]()
![]()
![]()
![]()
∵∠COE=∠DOE+∠COD=![]() +
+![]()
∴∠EOF=∠FOC+∠COE
=![]()
![]()
![]()
![]()
![]() +
+![]() +
+![]()
=![]() (
(![]() +
+![]() ).
).
③如图6,
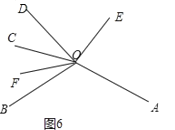
∠AOC=∠AOD+∠COD=2![]() +
+![]()
∵∠BOC=360![]() ∠AOB∠AOC
∠AOB∠AOC
=360![]()
![]() (2
(2![]() +
+![]() )
)
=360![]()
![]() 2
2![]()
![]()
∴∠FOC=![]() ∠BOC=180
∠BOC=180![]()
![]()
![]()
![]()
![]()
![]()
∵∠COE=∠DOE+∠COD=![]() +
+![]()
∴∠EOF=∠FOC+∠COE
=180![]()
![]()
![]()
![]()
![]()
![]() +
+![]() +
+![]()
=180![]()
![]() (
(![]()
![]() ).
).
④如图7,
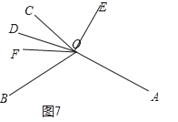
∠AOC=∠AOD∠COD=2![]()
![]()
∵∠BOC=360![]() ∠AOB∠AOC
∠AOB∠AOC
=360![]()
![]() (2
(2![]()
![]() )
)
=360![]()
![]() 2
2![]() +
+![]()
∴∠FOC=![]() ∠BOC=180
∠BOC=180![]()
![]()
![]()
![]() +
+![]()
![]()
∵∠COE=∠DOE∠COD=![]() β
β
∴∠EOF=∠FOC+∠COE
=180![]()
![]()
![]()
![]() +
+![]()
![]() +
+![]()
![]()
=180![]()
![]() (
(![]() +
+![]() ).
).
答:![]() 、β、∠EOF三者之间的数量关系为:
、β、∠EOF三者之间的数量关系为:![]() (
(![]()
![]() )、
)、![]() (
(![]() +
+![]() )、180
)、180![]()
![]() (
(![]()
![]() )、180
)、180![]()
![]() (
(![]() +
+![]() ).
).


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
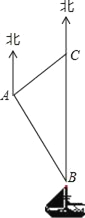
【题目】钓鱼岛是我国固有领土,现在我边海渔民要在钓鱼岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向20(1+![]() )海里的C处,为了防止某国海警干扰,请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向,A位于B的北偏西30°方向,求A、C之间的距离.
)海里的C处,为了防止某国海警干扰,请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向,A位于B的北偏西30°方向,求A、C之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,图①是沿
的中点,图①是沿![]() 将
将![]() 折叠,点
折叠,点![]() 落在
落在![]() 上,图②是绕点
上,图②是绕点![]() 将
将![]() 顺时针旋转
顺时针旋转![]() .
.
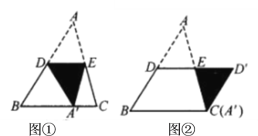
(1)在图①中,判断![]() 和
和![]() 形状.(填空)_______________________________________
形状.(填空)_______________________________________
(2)在图②中,判断四边形![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,斜坡AB的坡度![]() ,仰角∠CBE=50°.则山峰的高度CF约为( )米.(可用的参考数据:sin50°≈0.8,tan50°≈1.2,
,仰角∠CBE=50°.则山峰的高度CF约为( )米.(可用的参考数据:sin50°≈0.8,tan50°≈1.2, ![]() )
)
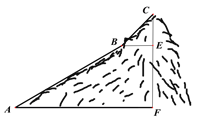
A. 500 B. 518 C. 530 D. 580
查看答案和解析>>
科目:初中数学 来源: 题型:
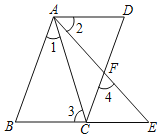
【题目】如图,已知四边形ABCD,AB∥CD,点E是BC延长线上一点,连接AC、AE,AE交CD于点F,∠1=∠2,∠3=∠4.
证明:
(1)∠BAE=∠DAC;
(2)∠3=∠BAE;
(3)AD∥BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价8折优惠;在乙超市累计购买商品超出200元之后超过部分按原价85折优惠设顾客预计累计购物![]() 元(
元(![]() )
)
(1)请用含![]() 的代数式分别表示顾客在两家超市购物所付的费用;
的代数式分别表示顾客在两家超市购物所付的费用;
(2)某顾客分别到两家超市买了相同的货物,并且所付费用也相同你知道这位顾客共花了多少钱吗?请列出方程解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数的图象经过![]() ,
,![]() 两点.
两点.
(1)求这个一次函数的解析式;
(2)试判断点![]() 是否在这个一次函数的图象上;
是否在这个一次函数的图象上;
(3)求此函数图象与![]() 轴,
轴,![]() 轴围成的三角形的面积.
轴围成的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平面内两点![]() .
.

(1)请用尺规按下列要求作图,并保留作图痕迹;
①连接![]() ;
;
②在线段![]() 的延长线上取点
的延长线上取点![]() ,使
,使![]() ;
;
③在线段![]() 的延长线上取点
的延长线上取点![]() ,使
,使![]() .
.
(2)请求出线段![]() 与线段
与线段![]() 长度之间的数量关系.
长度之间的数量关系.
(3)如果![]() ,则
,则![]() 的长度为________,
的长度为________,![]() 的长度为________,
的长度为________,![]() 的长度为_________.
的长度为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com