
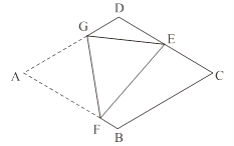
【题目】如图,在菱形纸片ABCD中,AB=2,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F、G分别在边AB、AD上.则cos∠EFG的值为________.
【答案】![]()
【解析】试题分析:作EH⊥AD于H,连接BE、BD,连接AE交FG于O,如图,
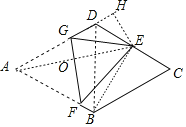
∵四边形ABCD为菱形,∠A=60°,
∴△BDC为等边三角形,∠ADC=120°,
∵E点为CD的中点,
∴CE=DE=1,BE⊥CD,
在Rt△BCE中,BE=![]() CE=
CE=![]() ,
,
∵AB∥CD,
∴BE⊥AB,
设AF=x,
∵菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F,G分别在边AB,AD上,
∴EF=AF,FG垂直平分AE,∠EFG=∠AFG,
在Rt△BEF中,(2-x)2+(![]() )2=x2,
)2=x2,
解得x=![]() ,
,
在Rt△DEH中,DH=![]() DE=
DE=![]() ,
,
HE=![]() DH=
DH=![]() ,
,
在Rt△AEH中,AE=![]() =
=![]() ,
,
∴AO=![]() ,
,
在Rt△AOF中,OF=![]() =
=![]() ,
,
∴cos∠AFO=![]() =
=![]() ,
,
∵∠EFG=∠AFO,
∴cos∠EFG=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】在“爱我永州”中学生演讲比赛中,五位评委分别给甲、乙两位选手的评分如下:
甲:8、7、9、8、8
乙:7、9、6、9、9
则下列说法中错误的是( )
A.甲、乙得分的平均数都是8
B.甲得分的众数是8,乙得分的众数是9
C.甲得分的中位数是9,乙得分的中位数是6
D.甲得分的方差比乙得分的方差小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们生活水平的提高,家用轿车越来越多地进入家庭,王先生家中买了一辆小轿车,他连接记录了7天中每天行驶的路程(如下表),以50km为标准,多于50km的记为“+”,不足50km的记为“-”,刚好50km的记为“0”.

(1)请求出这七天中平均每天行驶多少千米?
(2)若每行驶100km需用汽油6升,汽油价5.8元/升,请估计王先生家一个月(按30天计)的汽油费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
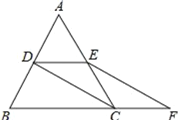
【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,过点E作EF∥CD交BC的延长线于点F,连接CD.
(1)求证:DE=CF;
(2)求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】滴滴打车为市民的出行带来了很大的方便,小亮调查了若干市民一周内使用滴滴打车的时间t(单位:分),将获得的数据分成四组,绘制了如下统计图,请根据图中信息,解答下列问题:
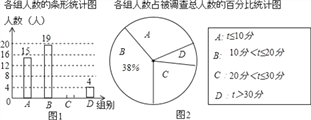
(1)这次被调查的总人数是多少?
(2)试求表示C组的扇形圆心角的度数,并补全条形统计图;
(3)若全市的总人数为666万,试求全市一周内使用滴滴打车超过20分钟的人数大约有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
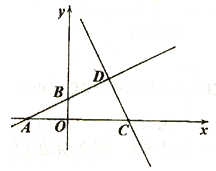
【题目】如图,已知A(-4,0)、B(0,2)、C(6,0),直线AB与直线CD相交于点D,D点的横纵坐标相同;
(1)求点D的坐标;
(2)点P从O出发,以每秒1个单位的速度沿x轴正半轴匀速运动,过点P作x轴的垂线分别与直线AB、CD交于E、F两点,设点P的运动时间为t秒,线段EF的长为y(y>0),求y与t之间的函数关系式,并直接写出自变量t的取值范围;
(3)在(2)的条件下,直线CD上是否存在点Q,使得△BPQ是以P为直角顶点的等腰直角三角形?若存在,请求出符合条件的Q点坐标,若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
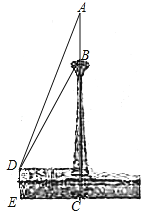
【题目】如图所示,天津电视塔顶部有一桅杆部分AB,数学兴趣小组的同学在距地面高为4.2m的平台D处观测电视塔桅杆顶部A的仰角为67.3°,观测桅杆底部B的仰角为58°.已知点A,B,C在同一条直线上,EC=172m.求测得的桅杆部分AB的高度和电视塔AC的高度.(结果保留小数点后一位).
参考数据:tan67.3°≈2.39,tan60°≈1.73.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体院要了解篮球专业学生投篮的命中率,对学生进行定点投篮测试,规定每人投篮20次,测试结束后随机抽查了一部分学生投中的次数,并分为五类,Ⅰ:投中11次;Ⅱ投中12次;Ⅲ:投中13次;Ⅳ:投中14次;Ⅴ:投中15次.根据调查结果绘制了下面尚不完整的统计图1、图2: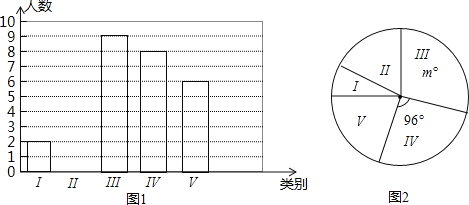
回答下列问题:
(1)本次抽查了 名学生,图2中的m= .
(2)补全条形统计图,并指出中位数在哪一类.
(3)求最高的命中率及命中最高的人数所占的百分比.
(4)若体院规定篮球专业学生定点投篮命中率不低于65%记作合格,估计该院篮球专业210名学生中约有多少人不合格.
查看答案和解析>>
科目:初中数学 来源: 题型:
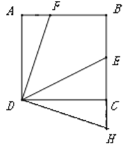
【题目】如图,正方形ABCD的边长为6,点E为BC的中点,点F在AB边上,![]() ,H在BC延长线上,且CH=AF,连接DF,DE,DH。
,H在BC延长线上,且CH=AF,连接DF,DE,DH。
(1)求证DF=DH;
(2)求![]() 的度数并写出计算过程.
的度数并写出计算过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com