
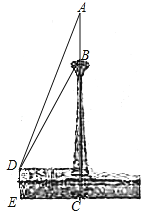
【题目】如图所示,天津电视塔顶部有一桅杆部分AB,数学兴趣小组的同学在距地面高为4.2m的平台D处观测电视塔桅杆顶部A的仰角为67.3°,观测桅杆底部B的仰角为58°.已知点A,B,C在同一条直线上,EC=172m.求测得的桅杆部分AB的高度和电视塔AC的高度.(结果保留小数点后一位).
参考数据:tan67.3°≈2.39,tan60°≈1.73.
【答案】桅杆部分AB的高度为135.9m,电视塔AC的高度为415.3m.
【解析】分析:
如下图,过点D作DF⊥AC于点F,由已知易得四边形DECF是矩形,由此可得DF=EC=172m,DE=CF=4.2m,然后在Rt△ADF和Rt△BDF中结合已知条件求得AF和BF的长,即可由AB=AF-BF和AC=AF+CF求得AB和AC的长了.
详解:
如图,作DF⊥AC于点F,

∵DF∥EC,DE∥CF,DE⊥EC,
∴四边形DECF是平行四边形,∠DEC=90°,
∴四边形DECF是矩形,
∴DF=EC=172m,DE=CF=4.2m,
∵∠ADF=67.3°,∠BDF=58°,
∴在Rt△ADF中,AF=DFtan67.3°≈411.1m,
在Rt△BDF中,BF=DFtan58°≈275.2m,
∴AB=AF﹣BF=411.1﹣275.2=135.9m,
AC=AF+CF=411.1+4.2=415.3m.
答:桅杆部分AB的高度为135.9m,天塔AC的高度为415.3m.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点.

(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应字母(保留作图痕迹,不写作法).
①作∠DAC的平分线AM;
②连接BE并延长交AM于点F;
③连接FC.
(2)猜想与证明:猜想四边形ABCF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知整数a1,a2,a3,a4,……滿足下列条件:a1=0,a2=-│a1+1│,a3=-│a2+2│,a4=-│a3+3│,·……,依次类推,则a2017的值为 ( )
A.-1007B.-1008C.-1009D.-2016
查看答案和解析>>
科目:初中数学 来源: 题型:
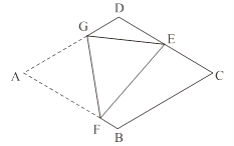
【题目】如图,在菱形纸片ABCD中,AB=2,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F、G分别在边AB、AD上.则cos∠EFG的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
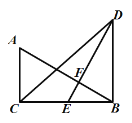
【题目】如图所示,在△ABC和△DBC中,∠ACB=∠DBC=90°,点E是BC的中点,EF⊥AB,垂足为F,且AB=DE.
(1)求证:△BCD是等腰直角三角形;
(2)若BD=8厘米,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为创建足球特色学校,营造足球文化氛围,某学校随机抽取部分八年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.(说明:A级:8分—10分,B级:7分—7.9分,C级:6分—6.9分,D级:1分—5.9分)根据所给信息,解答以下问题:
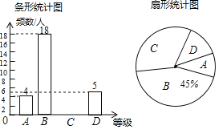
(1)样本容量为 ,C对应的扇形的圆心角是____度,补全条形统计图;
(2)所抽取学生的足球运球测试成绩的中位数会落在____等级;
(3)该校八年级有300名学生,请估计足球运球测试成绩达到![]() 级的学生有多少人?
级的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4 cm,BC=8 cm,点P从点D出发向点A运动,运动到点A即停止;同时点Q从点B出发向点C运动,运动到点C即停止.点P,Q的速度的速度都是1 cm/s,连结PQ,AQ,CP,设点P,Q运动的时间为t(s).
(1)当t为何值时,四边形ABQP是矩形?
(2)当t为何值时,四边形AQCP是菱形?
(3)分别求出(2)中菱形AQCP的周长和面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
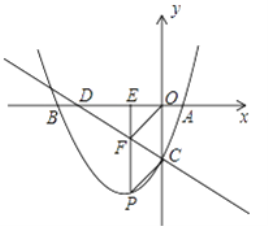
【题目】如图,已知抛物线y=ax2+ ![]() x+c与x轴交于A,B两点,与y轴交于丁C,且A(2,0),C(0,﹣4),直线l:y=﹣
x+c与x轴交于A,B两点,与y轴交于丁C,且A(2,0),C(0,﹣4),直线l:y=﹣ ![]() x﹣4与x轴交于点D,点P是抛物线y=ax2+
x﹣4与x轴交于点D,点P是抛物线y=ax2+![]() x+c上的一动点,过点P作PE⊥x轴,垂足为E,交直线l于点F.
x+c上的一动点,过点P作PE⊥x轴,垂足为E,交直线l于点F.
(1)试求该抛物线表达式;
(2)求证:点C在以AD为直径的圆上;
(3)是否存在点P使得四边形PCOF是平行四边形,若存在求出P点的坐标,不存在请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com