
【题目】如图,在直角坐标系中,矩形OABC的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E,那么点D的坐标为() 
A.(﹣ ![]() ,
, ![]() )
)
B.(﹣ ![]() ,
, ![]() )
)
C.(﹣ ![]() ,
, ![]() )
)
D.(﹣ ![]() ,
, ![]() )
)
【答案】C
【解析】解:如图,过D作DF⊥AF于F, ∵点B的坐标为(1,3),
∴AO=1,AB=3,
根据折叠可知:CD=OA,
而∠D=∠AOE=90°,∠DEC=∠AEO,
∴△CDE≌△AOE,
∴OE=DE,OA=CD=1,
设OE=x,那么CE=3﹣x,DE=x,
∴在Rt△DCE中,CE2=DE2+CD2 ,
∴(3﹣x)2=x2+12 ,
∴x= ![]() .
.
又DF⊥AF,
∴DF∥EO,
∴△AEO∽△ADF,
而AD=AB=3,
∴AE=CE=3﹣ ![]() =
= ![]() ,
,
∴ ![]() ,
,
即 ![]() ,
,
∴DF= ![]() ,AF=
,AF= ![]() .
.
∴OF= ![]() ﹣1=
﹣1= ![]() .
.
∴点D的坐标为(﹣ ![]() ,
, ![]() ).
).
故选:C.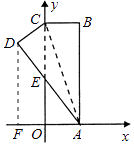
【考点精析】通过灵活运用矩形的性质和坐标与图形变化-对称,掌握矩形的四个角都是直角,矩形的对角线相等;关于x轴对称的点的特征:两个点关于x轴对称时,它们的坐标中,x相等,y的符号相反,即点P(x,y)关于x轴的对称点为P’(x,-y);关于y轴对称的点的特征:两个点关于y轴对称时,它们的坐标中,y相等,x的符号相反,即点P(x,y)关于y轴的对称点为P’(-x,y)即可以解答此题.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
【题目】如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.
(1)填空:与∠AOE互补的角有 ;
(2)若∠COD=30°,求∠DOE的度数;
(3)当∠AOD=α°时,请直接写出∠DOE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把四张大小相同的长方形卡片(如图1)按图2、图3两种方式放在一个底面为长方形(长比宽多7cm)的盒底上,底面未被卡片覆盖的部分用阴影表示,若记图2中阴影部分的周长为C1,图3中阴影部分的周长为C2,则C1比C2大_________ cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,直线a∥b,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上,且
上,且![]() ,
,![]() .点
.点![]() 、
、![]() 从
从![]() 点同时出发,分别以1个单位/秒,2个单位/秒的速度,在直线b上沿相反方向运动.设运动
点同时出发,分别以1个单位/秒,2个单位/秒的速度,在直线b上沿相反方向运动.设运动![]() 秒后,得到△ACD.(友情提醒:本题的结果可用根号表示)
秒后,得到△ACD.(友情提醒:本题的结果可用根号表示)
(1)当![]() 秒时,点
秒时,点![]() 到直线
到直线![]() 的距离为 ;
的距离为 ;
(2)若△ACD是直角三角形,t的值为 ;
(3)若△ACD是等腰三角形,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将正方形纸片ABCD沿FH折叠,使点D与AB的中点E重合,则△FAE与△EBG的面积之比为( ) 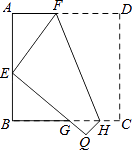
A.4:9
B.2:3
C.3:4
D.9:16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,从边长为a的正方形纸片中剪去一个边长为b的小正方形,则阴影部分的面积为 (写成两数平方差的形式);若将图1中的剩余纸片沿线段AB剪开,再把剪成的两张纸片拼成如图2的长方形,则长方形的面积是 (写成两个多项式相乘的形式);比较两图阴影部分的面积,可以得到一个公式: ;
(2)由此可知,通过图形的拼接可以验证一些等式.现在给你两张边长为a的正方形纸片、三张长为a,宽为b的长方形纸片和一张边长为b的正方形纸片(如图3所示),请你用这些纸片拼出一个长方形(所给纸片要用完),并写出它所验证的等式: .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com