
【题目】如图,在△ABC中,AB=AC,DE垂直平分AB.若BE⊥AC,AF⊥BC,垂足分别为点E,F,连接EF,则∠EFC=_____.
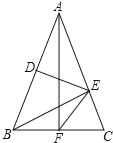
【答案】45°.
【解析】
先根据线段垂直平分线的性质及BE⊥AC得出△ABE是等腰直角三角形,再由等腰三角形的性质得出∠ABC的度数,由AB=AC,AF⊥BC,可知BF=CF,BF=EF;根据三角形外角的性质即可得出结论.
∵DE垂直平分AB,∴AE=BE.
∵BE⊥AC,∴△ABE是等腰直角三角形,∴∠BAC=∠ABE=45°.
又∵AB=AC,∴∠ABC![]() (180°﹣∠BAC)
(180°﹣∠BAC)![]() (180°﹣45°)=67.5°,∴∠CBE=∠ABC﹣∠ABE=67.5°﹣45°=22.5°.
(180°﹣45°)=67.5°,∴∠CBE=∠ABC﹣∠ABE=67.5°﹣45°=22.5°.
∵AB=AC,AF⊥BC,∴BF=CF,∴BF=EF;
∴∠BEF=∠CBE=22.5°,∴∠EFC=∠BEF+∠CBE=22.5°+22.5°=45°.
故答案为:45°.


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
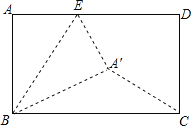
【题目】如图,长方形ABCD中,∠A=∠ABC=∠BCD=∠D=90°,AB=CD=6,AD=BC=10,点E为射线AD上的一个动点,若△ABE与△A′BE关于直线BE对称,当△A′BC为直角三角形时,AE的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E,那么点D的坐标为() 
A.(﹣ ![]() ,
, ![]() )
)
B.(﹣ ![]() ,
, ![]() )
)
C.(﹣ ![]() ,
, ![]() )
)
D.(﹣ ![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据图形填空:

(1)若直线ED,BC被直线AB所截,则∠1和__________是同位角.
(2)若直线ED,BC被直线AF所截,则∠3和__________是内错角.
(3)∠1和∠3是直线AB,AF被直线__________所截构成的__________角.
(4)∠2和∠4是直线__________,__________被直线BC所截构成的__________角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题。
(1)如图1,已知∠ACB=∠DCE=90°,AC=BC=6,CD=CE,AE=3,∠CAE=45°,求AD的长. 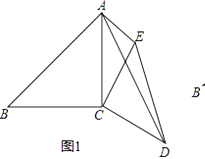
(2)如图2,已知∠ACB=∠DCE=90°,∠ABC=∠CED=∠CAE=30°,AC=3,AE=8,求AD的长. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的周长是20,OB和OC分别平分∠ABC和∠ACB,OD⊥BC于点D,且OD=3,则△ABC的面积是( )
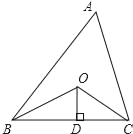
A. 20 B. 25 C. 30 D. 35
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗. 我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整). 请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE⊥BE,则线段CE的最小值为( ) 
A.![]()
B.2 ![]() ﹣2
﹣2
C.2 ![]() ﹣2
﹣2
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两种型号的机器加工同一种零件,已知A型机器比B型机器每小时多加工20个零件,A型机器加工400个零件所用时间与B型机器加工300个零件所用时间相同.A型机器每小时加工零件的个数_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com