练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在矩形ABCD中，AB=4，BC=6，E是矩形内部的一个动点，且AE⊥BE，则线段CE的最小值为（ ）
    A.
    B.2 ﹣2
    C.2 ﹣2
    D.4

    【答案】B
    【解析】解：如图，
    ∵AE⊥BE，
    ∴点E在以AB为直径的半⊙O上，
    连接CO交⊙O于点E′，
    ∴当点E位于点E′位置时，线段CE取得最小值，
    ∵AB=4，
    ∴OA=OB=OE′=2，
    ∵BC=6，
    ∴OC= = =2 ，
    则CE′=OC﹣OE′=2 ﹣2，
    故选：B．
    【考点精析】本题主要考查了矩形的性质和圆周角定理的相关知识点，需要掌握矩形的四个角都是直角，矩形的对角线相等；顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，将边长为a与b、对角线长为c的长方形纸片，绕点顺时针旋转得到长方形，连接，则四边形为梯形，请通过该图验证勾股定理（求证：）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB＝AC，DE垂直平分AB．若BE⊥AC，AF⊥BC，垂足分别为点E，F，连接EF，则∠EFC＝_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC 中，∠C＝90°，AD 是△ABC 的角平分线，DE⊥AB于 E，AC＝BE．

    （1）求证：AD＝BD；

    （2）求∠B的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知等腰直角△ABC，∠C＝90°，点D是斜边AB的中点，E是AC上的动点、∠EDF＝90°，DF交BC 于点F．

    （1）当 DE⊥AC，DF⊥BC 时，（如图1），我们很容易得出：S△DEF+S△CEF=S△ABC.

    （2）如图2，DE与 AC不垂直，且点E在线段AC上时，（1）中的结论是否成立，如果不成立，请说明理由；如果成立，请证明．

    （3）当点E运动到AC延长线上，其他条件不变，请把图3补充完整，直接写出 S△DEF，S△CEF，S△ABC的关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，∠AOB=30°，点A坐标为（2，0），过A作AA1⊥OB，垂足为点A1；过点A1作A1A2⊥x轴，垂足为点A2；再过点A2作A2A3⊥OB，垂足为点A3；则A2A3=；再过点A3作A3A4⊥x轴，垂足为点A4…；这样一直作下去，则A2017的纵坐标为 ．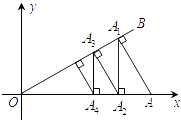

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，六边形ABCDEF的六个内角都相等．若AB=1，BC=CD=3，DE=2，则这个六边形的周长等于_________。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为实现区域教育均衡发展，我市计划对某县A、B两类薄弱学校全部进行改造，根据预算，共需资金1575万元，改造一所A类学校和两所B类学校共需资金230万元；改造两所A类学校和一所B类学校共需资金205万元.

    （1）改造一所A类学校和一所B类学校所需的资金分别是多少万元？

    （2）我市计划今年对该县A、B两类学校共6所进行改造，改造资金由国家财政和地方财政共同承担。若今年国家财政拨付的改造资金不超过400万元；地方财政投入的改造资金不少于70万元，其中地方财政投入到A、B两类学校的改造资金分别为每所10万元和15万元。请你通过计算求出有几种改造方案？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，等边△ABC的边长为12，D，E为BC的三等分点，M，N分别为AB，AC上的动点，则四边形DENM周长的最小值是_________.

    查看答案和解析>>

    同步练习册答案