
【题目】已知等腰直角△ABC,∠C=90°,点D是斜边AB的中点,E是AC上的动点、∠EDF=90°,DF交BC 于点F.
(1)当 DE⊥AC,DF⊥BC 时,(如图1),我们很容易得出:S△DEF+S△CEF=![]() S△ABC.
S△ABC.
(2)如图2,DE与 AC不垂直,且点E在线段AC上时,(1)中的结论是否成立,如果不成立,请说明理由;如果成立,请证明.
(3)当点E运动到AC延长线上,其他条件不变,请把图3补充完整,直接写出 S△DEF,S△CEF,S△ABC的关系.

【答案】(1)证明见解析;(2)成立;证明见解析;(3)S△DEF﹣S△CEF=![]() S△ABC.
S△ABC.
【解析】
(1)根据三角形的中位线和正方形的性质即可得到结论;
(2)如图 2,过 D作 DM⊥AC于 M,DN⊥BC于 N,根据三角形的中位线大小在得到 DM=DN,推出四边形 CNDM是正方形,得到 S正方形 DMCN=![]() S△ABC, 根据余角的性质得到∠EDM=∠FDN,根据全等三角形的性质得到△EDM≌△FDN,于是得到结论;
S△ABC, 根据余角的性质得到∠EDM=∠FDN,根据全等三角形的性质得到△EDM≌△FDN,于是得到结论;
(2)如图 3,过 D作 DM⊥AC于 M,DN⊥BC于 N,根据三角形的中位线大小在得到DM=DN,推出四边形 CNDM是正方形,得到 S正方形 DMCN=![]() S△ABC,根据余角的性质得到∠EDM=∠FDN,根据全等三角形的性质得到△EDM≌△FDN,于是得到结论.
S△ABC,根据余角的性质得到∠EDM=∠FDN,根据全等三角形的性质得到△EDM≌△FDN,于是得到结论.
(1)∵DE⊥AC,DF⊥BC,
∴DE∥BC,DF∥AC,
∵点D是斜边AB的中点,AC=BC,
∴DE=DF=![]() AC,
AC,
∴EF=![]() AB,
AB,
∴S△DEF+S△CEF=S四边形 DECF=![]() S△ABC;
S△ABC;
(2)结论仍然成立,
证明:如图2,过D作DM⊥AC于M,DN⊥BC于N,

∴∠AMC=∠DNC=∠C=90°,
∴DM∥BC,DN∥AC,
∵点D是斜边AB的中点,
∴DM=![]() BC,DN=
BC,DN=![]() AC,
AC,
∴DM=DN,
∴四边形CNDM是正方形,
∴S正方形DMCN=![]() S△ABC,
S△ABC,
∵∠EDF=90°,
∴∠EDM=∠FDN,
在△EDM与△FDN中,
∴△EDM≌△FDN,(ASA),
∴S四边形CFDE=S正方形DMCN=S△DEF+S△CEF=![]() S△ABC;
S△ABC;
(3)如图3,

过D作DM⊥AC于M,DN⊥BC于N,
∴∠AMC=∠DNC=∠C=90°,
∴DM∥BC,DN∥AC,
∵点D是斜边AB的中点,
∴DM=![]() BC,DN=
BC,DN=![]() AC,
AC,
∴DM=DN,
∴四边形CNDM是正方形,
∴S正方形DMCN=![]() S△ABC,
S△ABC,
∵∠EDF=90°,
∴∠EDM=∠FDN,
在△EDM与△FDN中, ,
,
∴△EDM≌△FDN,(ASA),
∴S四边形CFDE=S正方形DMCN=S△DEF﹣S△CEF=![]() S△ABC.
S△ABC.


 每课必练系列答案
每课必练系列答案科目:初中数学 来源: 题型:
【题目】已知实数a,b,c满足a+b=ab=c,有下列结论:①若c≠0,则![]() ;②若a=3,则b+c=9;③若c≠0,则(1-a)(1-b)=
;②若a=3,则b+c=9;③若c≠0,则(1-a)(1-b)=![]() ;④若c=5,则a2+b2=15. 其中正确的是( )
;④若c=5,则a2+b2=15. 其中正确的是( )
A. ①③④ B. ①②④ C. ①②③ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题。
(1)如图1,已知∠ACB=∠DCE=90°,AC=BC=6,CD=CE,AE=3,∠CAE=45°,求AD的长. 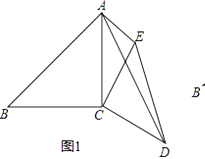
(2)如图2,已知∠ACB=∠DCE=90°,∠ABC=∠CED=∠CAE=30°,AC=3,AE=8,求AD的长. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗. 我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整). 请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:点B、F、C、E在一条直线上,FB=CE,AC=DF.能否由上面的已知条件证明AB∥ED?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件,添加到已知条件中,使AB∥ED成立,并给出证明.

供选择的三个条件(请从其中选择一个):
①AB=ED;
②BC=EF;
③∠ACB=∠DFE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE⊥BE,则线段CE的最小值为( ) 
A.![]()
B.2 ![]() ﹣2
﹣2
C.2 ![]() ﹣2
﹣2
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四张编号为A,B,C,D的卡片(除编号外,其余完全相同)的正面分别写上如图所示的正整数后,背面向上,洗匀放好. 
(1)我们知道,满足a2+b2=c2的三个正整数a,b,c成为勾股数,嘉嘉从中随机抽取一张,求抽到的卡片上的数是勾股数的概率P1;
(2)琪琪从中随机抽取一张(不放回),再从剩下的卡片中随机抽取一张(卡片用A,B,C,D表示).请用列表或画树形图的方法求抽到的两张卡片上的数都是勾股数的概率P2 , 并指出她与嘉嘉抽到勾股数的可能性一样吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小马虎解方理![]() =3出现了错误,解答过程如下:
=3出现了错误,解答过程如下:
方程两边都乘以x,得x﹣1+2=3(第一步)
移项,合并同类项,得x=2(第二步)
经检验,x=2是原方程的解(第三步)
(1)小马虎解答过程是从第 步开始出错的,出错原因是 ;
(2)请写出此题正确的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,AB是直径,OD⊥BC于点D,延长DO交⊙O于F,连接OC,AF. 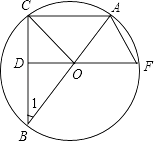
(1)求证:△COD≌△BOD;
(2)填空:①当∠1=时,四边形OCAF是菱形; ②当∠1=时,AB=2 ![]() OD.
OD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com