
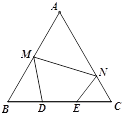
【题目】如图,等边△ABC的边长为12,D,E为BC的三等分点,M,N分别为AB,AC上的动点,则四边形DENM周长的最小值是_________.
【答案】20
【解析】
作D点关于AB的对称点D’、E点关于AC的对称点E’,连接D’E’分别与AB和AC交于M’和N’,则当M点运动至M’点、N点运动至N’点时,DM+MN+NE的最小值为D’E’,此时四边形DMNE的周长最小;分别作CC’⊥D’E’、BB’⊥D’E’,由对称及等边△ABC易知△N’CE’和△BM’D’均为等边三角形,由此可求解出D’E’的长度,进而求解四边形的周长.
解:作E点关于AC的对称点E’,过E’点作BC的平行线交AC于N’、交AB于M’,在直线E’M’上取D’点,连接BD’使BD’=BD,则当M点运动至M’点、N点运动至N’点时,DM+MN+NE的最小值为D’E’,此时四边形DMNE的周长最小;
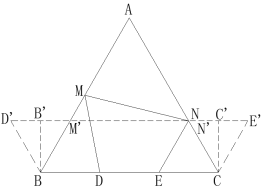
由对称性可知,∠N’CE=∠N’CE’=60°,
∵E’N’∥BC,
∴∠E’N’C=∠N’CE=∠N’CE’=60°,
∴△N’E’C是等边三角形,
∵E’D’∥BC,CE’=BD’,
∴四边形BCE’D’是等腰梯形,
∴∠D’=60°,
∵E’N’∥BC,
∴∠D’M’B=∠M’BD=60°,
∴△D’M’B是等边三角形,
分别作CC’⊥D’E’、BB’⊥D’E’,由图可知,D’E’长度等于BC长度再加上△N’E’C(或△D’M’B)的边长,则D’E’=12+4=16,
则四边形DENM周长的最小值=16+4=20.
故答案为:20.


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE⊥BE,则线段CE的最小值为( ) 
A.![]()
B.2 ![]() ﹣2
﹣2
C.2 ![]() ﹣2
﹣2
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两种型号的机器加工同一种零件,已知A型机器比B型机器每小时多加工20个零件,A型机器加工400个零件所用时间与B型机器加工300个零件所用时间相同.A型机器每小时加工零件的个数_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥EF,则∠A、∠C、∠D、∠E满足的数量关系是( )

A. ∠A+∠C+∠D+∠E=360°
B. ∠A+∠D=∠C+∠E
C. ∠A-∠C+∠D+∠E=180°
D. ∠E-∠C+∠D-∠A=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,AB是直径,OD⊥BC于点D,延长DO交⊙O于F,连接OC,AF. 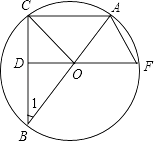
(1)求证:△COD≌△BOD;
(2)填空:①当∠1=时,四边形OCAF是菱形; ②当∠1=时,AB=2 ![]() OD.
OD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在日历上,我们可以发现其中某些数满足一定的规律.如图是2018年12月份的日历,我们任意选择其中所示的十字形部分,将每个部分中间数的左右两数,上下两数分别相乘,再把所得的结果相减.
(1)计算:11×13-5×19;16×18–10×24;(直接写结果)
(2)请你用整式的运算对以上的规律加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题:
(1)三条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(2)四条直线相交,最少有__________个交点,最多有__________个交点,分别画出图形,并数出图形中的对顶角和邻补角的对数;
(3)依次类推,n条直线相交,最少有__________个交点,最多有__________个交点,对顶角有__________对,邻补角有__________对.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某河大堤上有一颗大树ED,小明在A处测得树顶E的仰角为45°,然后沿坡度为1:2的斜坡AC攀行20米,在坡顶C处又测得树顶E的仰角为76°,已知ED⊥CD,并且CD与水平地面AB平行,求大树ED的高度.(精确到1米)
(参考数据:sin76°≈0.97,cos76°=0.24,tan76°≈4.01, ![]() =2.236)
=2.236)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在三角板ABC中,∠ACB=90°,∠A=30°,AC=6,将三角板ABC绕点C逆时针旋转,当起始位置时的点B恰好落在边A1B1上时,A1B的长为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com