
【题目】在△ABC中,点D为边BC上一点,请回答下列问题:

(1)如图1,若∠DAC=∠B,△ABC的角平分线CE交AD于点F,试说明∠AEF=∠AFE;
(2)在(1)的条件下,如图2,△ABC的外角∠ACQ的角平分线CP交BA的延长线于点P,若∠P=26°,猜想∠CFD的度数,并说明理由.
【答案】(1)证明见解析;(2)∠CFD=64°,理由见解析.
【解析】
(1)利用角平分线的定义可得出∠ECB=∠ACE,结合∠B=∠FAC可得出∠B+∠ECB=∠FAC+∠ACE,由三角形外角的性质可得出∠AEF=∠B+∠ECB,∠AFE=∠FAC+∠ACE,进而可得出∠AEF=∠AFE;
(2)由∠ACE=![]() ∠ACB,∠ACP=
∠ACB,∠ACP=![]() ∠ACQ,可得出∠ECP=90°,进而可得出∠P+∠AEC=90°,结合(1)的结论及对顶角相等可得出∠P+∠CFD=90°,代入∠P=26°即可求出∠CFD的度数.
∠ACQ,可得出∠ECP=90°,进而可得出∠P+∠AEC=90°,结合(1)的结论及对顶角相等可得出∠P+∠CFD=90°,代入∠P=26°即可求出∠CFD的度数.
解:(1)∵CE平分∠ACB,
∴∠ECB=∠ACE,
∵∠B=∠FAC,
∴∠B+∠ECB=∠FAC+∠ACE.
又∵∠AEF=∠B+∠ECB,∠AFE=∠FAC+∠ACE,
∴∠AEF=∠AFE.
(2)∠CFD=64°,理由如下:
∵∠ACE=![]() ∠ACB,∠ACP=
∠ACB,∠ACP=![]() ∠ACQ,
∠ACQ,
∴∠ECP=∠ACE+∠ACP=![]() (∠ACB+∠ACQ)=90°,
(∠ACB+∠ACQ)=90°,
∴∠P+∠AEC=90°.
∵∠AEF=∠AFE=∠CFD,
∴∠P+∠CFD=90°.
∵∠P=26°,
∴∠CFD=64°.


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x 2+bx+c与x轴交于A、B两点,与y轴交于点C,已知经过B、C两点的直线的表达式为y=-x+3.
(1)求抛物线的函数表达式;
(2)点P(m,0)是线段OB上的一个动点,过点P作y轴的平行线,交直线BC于D,交抛物线于E,EF∥x轴,交直线BC于F,DG∥x轴,FG∥y轴,DG与FG交于点G.设四边形DEFG的面积为S,当m为何值时S最大,最大值是多少?
(3)在坐标平面内是否存在点Q,将△OAC绕点Q逆时针旋转90°,使得旋转后的三角形恰好有两个顶点落在抛物线上.若存在,求出所有符合条件的点Q的坐标;若不存在,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,调查方式选择最合理的是![]()
![]()
A. 为了解安徽省中学生的课外阅读情况,选择全面调查
B. 调查七年级某班学生打网络游戏的情况,选择抽样调查
C. 为确保长征六号遥二火箭成功发射,应对零部件进行全面调查
D. 为了解一批袋装食品是否含有防腐剂,选择全面调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),公路上有A、B、C三个车站,一辆汽车从A站以速度v1匀速驶向B站,到达B站后不停留,以速度v2匀速驶向C站,汽车行驶路程y(千米)与行驶时间x(小时)之间的函数图象如图(2)所示.

(1)当汽车在A、B两站之间匀速行驶时,求y与x之间的函数关系式及自变量的取值范围;
(2)求出v2的值;
(3)若汽车在某一段路程内刚好用50分钟行驶了90千米,求这段路程开始时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .在同一平面直线坐标系中
.在同一平面直线坐标系中
(![]() )若函数
)若函数![]() 的图象过点
的图象过点![]() ,函数
,函数![]() 的图象过点
的图象过点![]() ,求
,求![]() ,
, ![]() 的值.
的值.
(![]() )若函数
)若函数![]() 的图象经过
的图象经过![]() 的顶点.
的顶点.
①求证: ![]() .
.
②当![]() 时,比较
时,比较![]() ,
, ![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将直角三角形ABC沿着BC方向平移![]() cm得到直角三角形DEF,AB=5cm,BC=8cm,DH=2cm,那么图中阴影部分的面积为____ cm 2.
cm得到直角三角形DEF,AB=5cm,BC=8cm,DH=2cm,那么图中阴影部分的面积为____ cm 2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线![]() :
:![]() 与直线
与直线![]() :
:![]() 都经过
都经过![]() ,直线
,直线![]() 交y轴于点
交y轴于点![]() ,交x轴于点A,直线
,交x轴于点A,直线![]() 交y轴于点D,P为y轴上任意一点,连接PA、PC,有以下说法:①方程组
交y轴于点D,P为y轴上任意一点,连接PA、PC,有以下说法:①方程组 的解为
的解为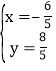 ;②
;②![]() 为直角三角形;③
为直角三角形;③![]() ;④当
;④当![]() 的值最小时,点P的坐标为
的值最小时,点P的坐标为![]() 其中正确的说法个数有
其中正确的说法个数有![]()
![]()
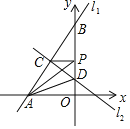
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现如今,通过“微信运动“发布自己每天行走的步数,已成为一种时尚,“健身达人”小华为了了解他的微信朋友圈里大家的“建步走运动“情况,随机抽取了20名好友一天行走的步数,记录如下:
5640 | 6430 | 6320 | 6798 | 7325 | 8430 | 8215 | 7453 | 7446 | 6754 |
7638 | 6834 | 7325 | 6830 | 8648 | 8753 | 9450 | 9865 | 7290 | 7850 |
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
组别 | 步数分组 | 频数 |
A | 5500≤x<6500 | 2 |
B | 6500≤x<7500 | 10 |
C | 7500≤x | m |
D | 8500≤x<9500 | 2 |
E | 9500≤x<10500 | n |
请根据以上信息解答下列问题:
(1)填空:m= ,n= .
(2)补全频数分布直方图.
(3)根据以上统计结果,第二天小华随机查看一名好友行走的步数,试估计该好友的步数不低于7500步(含7500步)的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个正整数能表示成两个连续偶数的平方差,那么这个正整数为“神秘数”.
如:![]()
![]()
![]()
因此,4,12,20这三个数都是神秘数.
(1)28和2012这两个数是不是神秘数?为什么?
(2)设两个连续偶数为![]() 和
和![]() (其中
(其中![]() 为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
(3)两个连续奇数的平方差(取正数)是不是神秘数?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com