
【题目】现如今,通过“微信运动“发布自己每天行走的步数,已成为一种时尚,“健身达人”小华为了了解他的微信朋友圈里大家的“建步走运动“情况,随机抽取了20名好友一天行走的步数,记录如下:
5640 | 6430 | 6320 | 6798 | 7325 | 8430 | 8215 | 7453 | 7446 | 6754 |
7638 | 6834 | 7325 | 6830 | 8648 | 8753 | 9450 | 9865 | 7290 | 7850 |
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
组别 | 步数分组 | 频数 |
A | 5500≤x<6500 | 2 |
B | 6500≤x<7500 | 10 |
C | 7500≤x | m |
D | 8500≤x<9500 | 2 |
E | 9500≤x<10500 | n |
请根据以上信息解答下列问题:
(1)填空:m= ,n= .
(2)补全频数分布直方图.
(3)根据以上统计结果,第二天小华随机查看一名好友行走的步数,试估计该好友的步数不低于7500步(含7500步)的概率.

 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
【题目】如图,将边长为![]() 的菱形ABCD纸片放置在平面直角坐标系中.已知∠ABO=45°.
的菱形ABCD纸片放置在平面直角坐标系中.已知∠ABO=45°.
(1)求出点B、C的坐标;
(2)设边AB沿y轴对折后的对应线段为AB′,求出点B′的坐标及线段CB′的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,点D为边BC上一点,请回答下列问题:

(1)如图1,若∠DAC=∠B,△ABC的角平分线CE交AD于点F,试说明∠AEF=∠AFE;
(2)在(1)的条件下,如图2,△ABC的外角∠ACQ的角平分线CP交BA的延长线于点P,若∠P=26°,猜想∠CFD的度数,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF=![]() DC,连接EF并延长交BC的延长线于点G。
DC,连接EF并延长交BC的延长线于点G。
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程k2x2﹣2(k+1)x+1=0有两个实数根.
(1)求k的取值范围;
(2)当k=1时,设所给方程的两个根分别为x1和x2,求(x1﹣2)(x2﹣2)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)我国著名的数学家赵爽,早在公元3世纪,就把一个矩形分成四个全等的直角三角形,用四个全等的直角三角形拼成丁一个大的正方形(如图1),这个矩形称为赵爽弦图,验证了一个非常重要的结论:在直角三角形中两直角边a、b与斜边c满足关系式a2+b2=c2,称为勾股定理.
证明:∵大正方形面积表示为S=c2,,又可表示为S=4×![]() ab+(b-a)2,
ab+(b-a)2,
∴4×![]() ab+(b-a)2=c2.
ab+(b-a)2=c2.
∴______________
即直角三角形两直角边的平方和等于斜边的平方.
(2)爱动脑筋的小明把这四个全等的直角三角形拼成了另一个大的正方形(如图2),也能验证这个结论,请你帮助小明完成验证的过程.
(3)如图3所示,∠ABC=∠ACE=90°,请你添加适当的辅助线,证明结论a2+b2=c2.

查看答案和解析>>
科目:初中数学 来源: 题型:
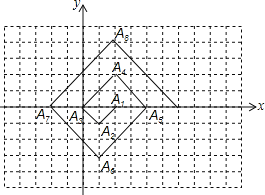
【题目】如图,在一个单位面积为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,……是斜边在x轴上,且斜边长分别为2,4,6,……的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,点A2019的横坐标为( )
A. 1010B. ![]() C. 1008D.
C. 1008D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() :
:![]() 和直线
和直线![]() :
:![]() ,过点
,过点![]() 作
作![]() 轴,交直线
轴,交直线![]() 于点A,若点P是x轴上的一个动点,过点P作平行于y轴的直线,分别与
于点A,若点P是x轴上的一个动点,过点P作平行于y轴的直线,分别与![]() 、
、![]() 交于点C、D,连接AD、BC.
交于点C、D,连接AD、BC.
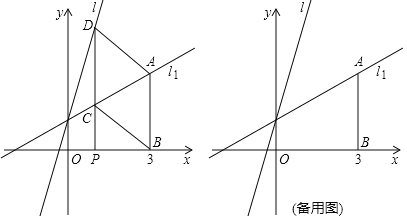
![]() 直接写出线段
直接写出线段![]() ______;
______;
![]() 当P的坐标是
当P的坐标是![]() 时,求直线BC的解析式;
时,求直线BC的解析式;
![]() 若
若![]() 的面积与
的面积与![]() 的面积相等,求点P的坐标.
的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点A、C、D在⊙O上,BP是⊙O的切线,连接PD并延长交⊙O于F、交AB于E,若∠BPF=∠ADC.
(1)判断直线PF与AC的位置关系,并说明你的理由;
(2)当⊙O的半径为5,tan∠P=![]() ,求AC的长.
,求AC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com