
 如图,Rt△ABO的斜边OA在x轴上,点B在第一象限内,OA:OB=5:4,边AB的垂直平分线分别交 AB、x轴于点C、D,线段CD交反比例函数y=
如图,Rt△ABO的斜边OA在x轴上,点B在第一象限内,OA:OB=5:4,边AB的垂直平分线分别交 AB、x轴于点C、D,线段CD交反比例函数y=| 3 |
| x |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 29 |
| 10 |
| 3 |
| 10 |
| 3 |
| x |
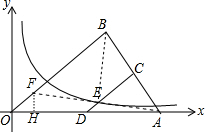
| OA2-OB2 |
| 1 |
| 2 |
| 3 |
| 2 |
| FH |
| AB |
| OH |
| OB |
| OF |
| OA |
| FH |
| 3x |
| OH |
| 4x |
| x |
| 5x |
| 3 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| 29 |
| 10 |
| 3 |
| 10 |
| 29 |
| 10 |
| 3 |
| 10 |
| 3 |
| x |
| 29 |
| 10 |
| 3 |
| 10 |
10
| ||
| 29 |
| 29 |
3
| ||
| 29 |
| 29 |
3
| ||
| 29 |


科目:初中数学 来源: 题型:
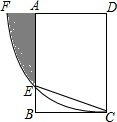 如图,在矩形ABCD中,AD=2
如图,在矩形ABCD中,AD=2| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
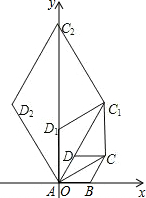 如图,边长为1的菱形ABCD中,A在原点,B在x轴正半轴上,∠DAB=60°.连接对角线AC,以AC为边作第二个菱形ACC1D1,∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°,…,C、C1、C2、C3…按逆时针方向排列,按此规律所作的第2015个菱形AC2013C2014D2014的顶点C2014的坐标为
如图,边长为1的菱形ABCD中,A在原点,B在x轴正半轴上,∠DAB=60°.连接对角线AC,以AC为边作第二个菱形ACC1D1,∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°,…,C、C1、C2、C3…按逆时针方向排列,按此规律所作的第2015个菱形AC2013C2014D2014的顶点C2014的坐标为查看答案和解析>>
科目:初中数学 来源: 题型:
 学校组织学生外出踏青,学生队伍从学校先步行出发,一段时间后王老师从学校骑车追赶学生,追上学生时接到电话要求王老师返回,因此王老师又立即按原速返回,当王老师回到学校时,学生还在继续前行,直到目的地.设王老师和学生队伍间的距离为y米,从王老师出发开始计时,设时间为x分钟,图中折线表示y与x的函数关系,则王老师比学生队伍的速度快
学校组织学生外出踏青,学生队伍从学校先步行出发,一段时间后王老师从学校骑车追赶学生,追上学生时接到电话要求王老师返回,因此王老师又立即按原速返回,当王老师回到学校时,学生还在继续前行,直到目的地.设王老师和学生队伍间的距离为y米,从王老师出发开始计时,设时间为x分钟,图中折线表示y与x的函数关系,则王老师比学生队伍的速度快查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com