
【题目】如图,梯形ABCD的对角线AC、BD相交于O,点H为BC上一点,连接AH交BD于点G.若AD=3,BC=9,BH:HC=1:2,则GO:BG=( )
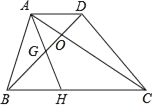
A.1:2B.1:3C.2:3D.11:20
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=6,AD=8,点E是边AD上一点,EM⊥BC交AB于点M,点N在射线MB上,且AE是AM和AN的比例中项.
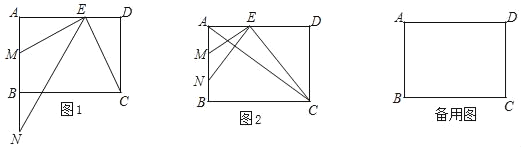
(1)如图1,求证:∠ANE=∠DCE;
(2)如图2,当点N在线段MB之间,联结AC,且AC与NE互相垂直,求MN的长;
(3)连接AC,如果△AEC与以点E、M、N为顶点所组成的三角形相似,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B处的求救者后,又发现点B正上方点C处还有一名求救者.在消防车上点A处测得点B和点C的仰角分别是45°和65°,点A距地面2.5米,点B距地面10.5米.为救出点C处的求救者,云梯需要继续上升的高度BC约为多少米?(结果保留整数.参考数据:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,![]() ≈1.4)
≈1.4)

查看答案和解析>>
科目:初中数学 来源: 题型:
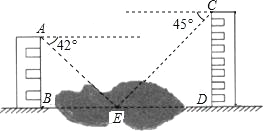
【题目】如图,两幢建筑物AB和CD,AB⊥BD,CD⊥BD,AB=15m,CD=20m.AB和CD之间有一景观池,小双在A点测得池中喷泉处E点的俯角为42°,在C点测得E点的俯角为45°,点B、E、D在同一直线上.求两幢建筑物之间的距离BD.(结果精确到0.1m)(参考数据:sin42°=0.67,cos42°=0.74,tan42°=0.90)
查看答案和解析>>
科目:初中数学 来源: 题型:
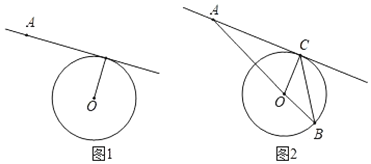
【题目】如图1,点A是⊙O外一点.
(1)过点A作⊙O的切线(要求:尺规作图,保留作图痕迹,不写作法);
(2)如图2,设AC是⊙O的切线,点C是切点,已知tan∠A=![]() ,求tan∠ABC的值.
,求tan∠ABC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以坐标原点O为圆心,2为半径画圆,P是⊙O上一动点且在第一象限内,过点P作⊙O的切线,与x、y轴分别交于点A、B.
(1)求证:△OBP与△OPA相似;
(2)当点P为AB中点时,求出P点坐标;
(3)在⊙O上是否存在一点Q,使得以Q,O,A、P为顶点的四边形是平行四边形.若存在,试求出Q点坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在实施“棚户区”改造工程中,我市计划推出![]() 、
、![]() 两种新户型.根据预算,建成10套
两种新户型.根据预算,建成10套![]() 种户型和30套
种户型和30套![]() 种户型住房共需资金2790万元,建成30套
种户型住房共需资金2790万元,建成30套![]() 种户型和10套
种户型和10套![]() 种户型住房共需资金2130万元.
种户型住房共需资金2130万元.
(1)在危旧房改造中建成一套![]() 种户型和一套
种户型和一套![]() 种户型住房所需资金分别是多少万元?
种户型住房所需资金分别是多少万元?
(2)河西区有200套住房需要改造,改造资金由国家危旧房补贴和地方财政共同承担,若国家危旧房补贴拨付的改造资金不超过6560万元,地方财政投入额资金不少于5050万元,其中国家危旧房补贴投入到![]() 、
、![]() 两种户型的改造资金分别为每套27万元和40万元
两种户型的改造资金分别为每套27万元和40万元
①请你设计出改造方案:
②设这项改造工程总投入资金![]() 万元,建成
万元,建成![]() 种户型
种户型![]() 套,写出
套,写出![]() 与
与![]() 的关系式,并求出最少总投入.
的关系式,并求出最少总投入.
查看答案和解析>>
科目:初中数学 来源: 题型:
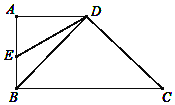
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AB=AD,连接BD,点E在AB上,且∠BDE=15°,DE=4![]() ,DC=2
,DC=2![]() .
.
(1)求BE的长;
(2)求四边形DEBC的面积.
(注意:本题中的计算过程和结果均保留根号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com