
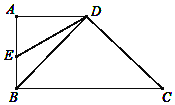
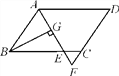
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AB=AD,连接BD,点E在AB上,且∠BDE=15°,DE=4![]() ,DC=2
,DC=2![]() .
.
(1)求BE的长;
(2)求四边形DEBC的面积.
(注意:本题中的计算过程和结果均保留根号)
【答案】(1)BE=6﹣2![]() ;(2)S四边形DEBC=36+6
;(2)S四边形DEBC=36+6![]() .
.
【解析】
(1)解直角三角形求出AD、AE即可解决问题;
(2)作DF⊥BC于F.则四边形ABFD是矩形,解直角三角形求出CF,即可解决问题;
(1)在四边形ABCD中,∵AD∥BC,∠ABC=90°,
∴∠BAD=90°,
∵AB=AD,
∴∠ABD=∠ADB=45°,
∵∠BDE=15°,
∴∠ADE=30°,
在Rt△ADE中,AE=DE×sin30=2![]() ,AD=DEcos30°=6,
,AD=DEcos30°=6,
∴AB=AD=6,
∴BE=6﹣2![]() .
.
(2)作DF⊥BC于F.则四边形ABFD是矩形,

∴BF=AD=6,DF=AB=6,
在Rt△DFC中,FC=![]() ,
,
∴BC=6+4![]() ,
,
∴S四边形DEBC=S△DEB+S△BCD=![]() ×(6﹣2
×(6﹣2![]() )×6+
)×6+![]() (6+4
(6+4![]() )×6=36+6
)×6=36+6![]() .
.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:
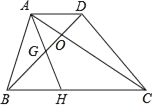
【题目】如图,梯形ABCD的对角线AC、BD相交于O,点H为BC上一点,连接AH交BD于点G.若AD=3,BC=9,BH:HC=1:2,则GO:BG=( )
A.1:2B.1:3C.2:3D.11:20
查看答案和解析>>
科目:初中数学 来源: 题型:
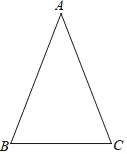
【题目】在△ABC中,AB=AC
(1)利用直尺和圆规完成如下操作,作∠BAC的平分线和AB的垂直平分线,交点为P(不写作法,保留作图瘕迹)
(2)连结PB,若∠ABC=65°,求∠ABP的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
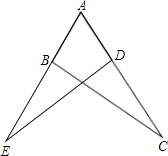
【题目】如图,点B在AE上,点D在AC上,AB=AD.请你添加一个适当的条件,使△ABC≌△ADE(只能添加一个).
(1)你添加的条件是 .
(2)添加条件后,请说明△ABC≌△ADE的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】柳州市某校的生物兴趣小组在老师的指导下进行了多项有意义的生物研究并取得成果.下面是这个兴趣小组在相同的实验条件下,对某植物种子发芽率进行研究时所得到的数据:
种子数 | 30 | 75 | 130 | 210 | 480 | 856 | 1250 | 2300 |
发芽数 | 28 | 72 | 125 | 200 | 457 | 814 | 1187 | 2185 |
发芽频率 | 0.9333 | 0.9600 | 0.9615 | 0.9524 | 0.9521 | 0.9509 | 0.9496 | 0.9500 |
依据上面的数据可以估计,这种植物种子在该实验条件下发芽的概率约是_____(结果精确到0.01).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于点G,BG=4![]() ,则△EFC的周长为( )
,则△EFC的周长为( )
A. 11 B. 10 C. 9 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛一枚均匀硬币正面朝上的概率为![]() ,下列说法错误的是
,下列说法错误的是![]()
![]()
A. 连续抛一枚均匀硬币2次必有1次正面朝上
B. 连续抛一枚均匀硬币10次都可能正面朝上
C. 大量反复抛一枚均匀硬币,平均每100次出现正面朝上50次
D. 通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011山东济南,27,9分)如图,矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线![]() 经过A、C两点,与AB边交于点D.
经过A、C两点,与AB边交于点D.
(1)求抛物线的函数表达式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式,并求出m为何值时,S取得最大值;
②当S最大时,在抛物线![]() 的对称轴l上若存在点F,使△FDQ为直角三角形,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.
的对称轴l上若存在点F,使△FDQ为直角三角形,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点 A 在函数y1=-![]() (x>0)的图象上,点 B 在直线 y2=kx+1+k(k 为常数,且 k≥0)上.若 A,B 两点关于原点对称,则称点 A,B 为函数 y1,y2 图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )
(x>0)的图象上,点 B 在直线 y2=kx+1+k(k 为常数,且 k≥0)上.若 A,B 两点关于原点对称,则称点 A,B 为函数 y1,y2 图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为( )
A.有1对或2对B.只有1对
C.只有2对D.有2对或3对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com