
【题目】如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于点G,BG=4![]() ,则△EFC的周长为( )
,则△EFC的周长为( )
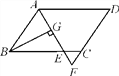
A. 11 B. 10 C. 9 D. 8
【答案】D
【解析】试题分析:判断出△ADF是等腰三角形,△ABE是等腰三角形,DF的长度,继而得到EC的长度,在Rt△BGE中求出GE,继而得到AE,求出△ABE的周长,根据相似三角形的周长之比等于相似比,可得出△EFC的周长.
∵在ABCD中,AB=CD=6,AD=BC=9,∠BAD的平分线交BC于点E,
∴∠BAF=∠DAF,
∵AB∥DF,AD∥BC,
∴∠BAF=∠F=∠DAF,∠BAE=∠AEB,
∴AB=BE=6,AD=DF=9,
∴△ADF是等腰三角形,△ABE是等腰三角形,
∵AD∥BC,
∴△EFC是等腰三角形,且FC=CE,
∴EC=FC=9﹣6=3,
在△ABG中,BG⊥AE,AB=6,BG=![]() ,
,
∴AG=![]() =2,
=2,
∴AE=2AG=4,
∴△ABE的周长等于16,
又∵△CEF∽△BEA,相似比为1:2,
∴△CEF的周长为8.
故选D.


科目:初中数学 来源: 题型:
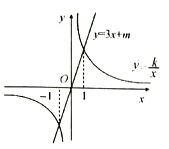
【题目】将直线y=3x+1向下平移1个单位长度,得到直线y=3x +m,若反比例函数![]() 的图象与直线y=3x+m相交于点A,且点A 的纵坐标是3.
的图象与直线y=3x+m相交于点A,且点A 的纵坐标是3.
(1)求m和k的值;
(2) 直接写出方程![]() 的解:
的解:
(3) 结合图象求不等式![]() 的解集
的解集
查看答案和解析>>
科目:初中数学 来源: 题型:
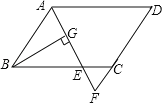
【题目】如图,已知![]() ,
,![]() ,点
,点![]() 是射线
是射线![]() 上一动点(与点
上一动点(与点![]() 不重合),
不重合),![]() 分别平分
分别平分![]() 和
和![]() ,分别交射线
,分别交射线![]() 于点
于点![]() .
.

(1)![]() ;
;![]() ;
;
(2)当点![]() 运动到某处时,
运动到某处时,![]() ,求此时
,求此时![]() 的度数.
的度数.
(3)当点![]() 运动时,
运动时,![]() :
:![]() 的比值是否随之变化?若不变,请求出这个比值;若变化,请找出变化规律;
的比值是否随之变化?若不变,请求出这个比值;若变化,请找出变化规律;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于频率与概率有下列几种说法:①“明天下雨的概率是90%”表示明天下雨的可能性很大;②“抛一枚硬币正面朝上的概率为![]() ”表示每抛两次就有一次正面朝上;③“某彩票中奖的概率是1%”表示买10张该种彩票不可能中奖;④“抛一枚硬币正面朝上的概率为
”表示每抛两次就有一次正面朝上;③“某彩票中奖的概率是1%”表示买10张该种彩票不可能中奖;④“抛一枚硬币正面朝上的概率为![]() ”表示随着抛掷次数的增加,“抛出正面朝上”这一事件发生的频率稳定在
”表示随着抛掷次数的增加,“抛出正面朝上”这一事件发生的频率稳定在![]() 附近,正确的说法是( )
附近,正确的说法是( )
A. ②④B. ②③C. ①④D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】★若两个扇形满足弧长的比等于它们半径的比,则称这两个扇形相似.如图,如果扇形AOB与扇形A1O1B1是相似扇形,且半径OA∶O1A1=k(k为不等于0的常数).那么下面四个结论:①∠AOB=∠A1O1B1;②△AOB∽△A1O1B1;③![]() =k;④扇形AOB与扇形A1O1B1的面积之比为k2.成立的个数为( )
=k;④扇形AOB与扇形A1O1B1的面积之比为k2.成立的个数为( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荣昌公司要将本公司100吨货物运往某地销售,经与春晨运输公司协商,计划租用甲、乙两种型号的汽车共6辆,用这6辆汽车一次将货物全部运走,其中每辆甲型汽车最多能装该种货物16吨,每辆乙型汽车最多能装该种货物18吨.已知租用1辆甲型汽车和2辆乙型汽车共需费用2500元;租用2辆甲型汽车和1辆乙型汽车共需费用2450元,且同一种型号汽车每辆租车费用相同.
(1)求租用一辆甲型汽车、一辆乙型汽车的费用分别是多少元?
(2)若荣昌公司计划此次租车费用不超过5000元.通过计算求出该公司有几种租车方案?请你设计出来,并求出最低的租车费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在今年我市初中学业水平考试体育学科的女子800米耐力测试中,某考点同时起跑的小莹和小梅所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,下列说法正确的是( )
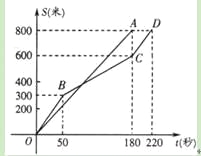
A. 小莹的速度随时间的增大而增大B. 小梅的平均速度比小莹的平均速度大
C. 在起跑后180秒时,两人相遇D. 在起跑后50秒时,小梅在小莹的前面
查看答案和解析>>
科目:初中数学 来源: 题型:
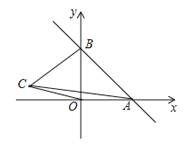
【题目】如图,一次函数y=kx+b的图象分别与x轴,y轴的正半轴分別交于点A,B,AB=2![]() ,∠OAB=45°
,∠OAB=45°
(1)求一次函数的解析式;
(2)如果在第二象限内有一点C(a,![]() );试用含有a的代数式表示四边形ABCO的面积,并求出当△ABC的面积与△ABO的面积相等时a的值;
);试用含有a的代数式表示四边形ABCO的面积,并求出当△ABC的面积与△ABO的面积相等时a的值;
(3)在x轴上,是否存在点P,使△PAB为等腰三角形?若存在,请直接写出所有符合条件的点P坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com