
ĄžĚâÄżĄżÔÚʾʊĄ°ĹÇřĄą¸ÄÔ욤łĚÖĐŁŹÎŇĘПƝŽÍĆłö![]() Ą˘
Ą˘![]() Á˝ÖÖĐÂť§ĐÍ.¸ůžÝÔ¤Ë㣏˝¨łÉ10Ě×
Á˝ÖÖĐÂť§ĐÍ.¸ůžÝÔ¤Ë㣏˝¨łÉ10Ě×![]() ÖÖť§ĐÍşÍ30Ě×
ÖÖť§ĐÍşÍ30Ě×![]() ÖÖť§ĐÍץˇżš˛Đč×Ę˝đ2790ÍňÔŞŁŹ˝¨łÉ30Ě×
ÖÖť§ĐÍץˇżš˛Đč×Ę˝đ2790ÍňÔŞŁŹ˝¨łÉ30Ě×![]() ÖÖť§ĐÍşÍ10Ě×
ÖÖť§ĐÍşÍ10Ě×![]() ÖÖť§ĐÍץˇżš˛Đč×Ę˝đ2130ÍňÔŞ.
ÖÖť§ĐÍץˇżš˛Đč×Ę˝đ2130ÍňÔŞ.
Ł¨1ŁŠÔÚÎŁžÉˇż¸ÄÔěÖĐ˝¨łÉŇťĚ×![]() ÖÖť§ĐÍşÍŇťĚ×
ÖÖť§ĐÍşÍŇťĚ×![]() ÖÖť§ĐÍץˇżËůĐč×Ę˝đˇÖąđĘÇśŕÉŮÍňÔŞŁż
ÖÖť§ĐÍץˇżËůĐč×Ę˝đˇÖąđĘÇśŕÉŮÍňÔŞŁż
Ł¨2ŁŠşÓÎ÷ÇřÓĐ200Ě×ץˇżĐčŇŞ¸ÄÔ죏¸ÄÔě×Ę˝đÓÉšúźŇÎŁžÉˇż˛šĚůşÍľŘˇ˝˛ĆŐţš˛ÍŹłĐľŁŁŹČôšúźŇÎŁžÉˇż˛šĚů˛Ś¸śľÄ¸ÄÔě×ʽ𲝳Źšý6560ÍňÔŞŁŹľŘˇ˝˛ĆŐţÍśČëśî×Ę˝đ˛ťÉŮÓÚ5050ÍňÔŞŁŹĆäÖĐšúźŇÎŁžÉˇż˛šĚůÍśČëľ˝![]() Ą˘
Ą˘![]() Á˝ÖÖť§Đ;ĸÄÔě×Ę˝đˇÖąđÎŞĂżĚ×27ÍňÔŞşÍ40ÍňÔŞ
Á˝ÖÖť§Đ;ĸÄÔě×Ę˝đˇÖąđÎŞĂżĚ×27ÍňÔŞşÍ40ÍňÔŞ
˘ŮÇëÄăÉčźĆłö¸ÄÔ졽°¸Łş
˘ÚÉčŐâĎî¸ÄÔ욤łĚ×ÜÍśČë×Ę˝đ![]() ÍňÔŞŁŹ˝¨łÉ
ÍňÔŞŁŹ˝¨łÉ![]() ÖÖť§ĐÍ
ÖÖť§ĐÍ![]() ĚףŹĐ´łö
ĚףŹĐ´łö![]() Óë
Óë![]() ľÄšŘϾʽŁŹ˛˘Çółö×îÉŮ×ÜÍśČë.
ľÄšŘϾʽŁŹ˛˘Çółö×îÉŮ×ÜÍśČë.
Ąž´đ°¸ĄżŁ¨1ŁŠÔÚÎŁžÉˇż¸ÄÔěÖĐ˝¨łÉŇťĚ×![]() ÖÖť§ĐÍşÍŇťĚ×
ÖÖť§ĐÍşÍŇťĚ×![]() ť§ĐÍץˇżËůĐč×Ę˝đˇÖąđĘÇ45ÍňÔŞşÍ78ÍňÔŞŁťŁ¨2ŁŠ˘Ůš˛ÓĐ17ÖָĽ¨ˇ˝°¸Łť˘Úľą
ť§ĐÍץˇżËůĐč×Ę˝đˇÖąđĘÇ45ÍňÔŞşÍ78ÍňÔŞŁťŁ¨2ŁŠ˘Ůš˛ÓĐ17ÖָĽ¨ˇ˝°¸Łť˘Úľą![]() ĘąŁŹ
ĘąŁŹ![]()
![]() Ł¨ÍňÔŞŁŠ.
Ł¨ÍňÔŞŁŠ.
Ąž˝âÎöĄż
Ł¨1ŁŠ¸ůžÝ˝¨łÉ10Ě×AÖÖť§ĐÍşÍ30Ě×BÖÖť§ĐÍץˇżš˛Đč×Ę˝đ2790ÍňÔŞŁŹ˝¨łÉ30Ě×AÖÖť§ĐÍşÍ10Ě×BÖÖť§ĐÍץˇżš˛Đč×Ę˝đ2130ÍňÔŞŁŹżÉŇÔÁĐłöĎŕÓŚľÄśţÔŞŇť´Îˇ˝łĚ×飏´ÓśřżÉŇÔÇóľĂÔÚÎŁžÉˇż¸ÄÔěÖĐ˝¨łÉŇťĚ×AÖÖť§ĐÍşÍŇťĚ×BÖÖť§ĐÍץˇżËůĐč×Ę˝đˇÖąđĘÇśŕÉŮÍňÔŞŁť
Ł¨2ŁŠ˘ŮŁŹ¸ůžÝĚâŇâżÉŇÔÁĐłöĎŕÓŚľÄ˛ťľČĘ˝×飏´ÓśřżÉŇÔ˝â´đąžĚ⣝
˘Ú¸ůžÝĚâŇâżÉŇÔĐ´łöWÓëmľÄşŻĘýšŘϾʽŁŹÔٸůžÝ˘ŮÖоĽášűź´żÉ˝â´đąžĚ⣎
ĚâÄż×÷ÁËĐ޸ĞͲοźČçĎ¾Ĵ𰸣ş
Ł¨1ŁŠÉčÔÚÎŁžÉˇż¸ÄÔěÖĐ˝¨łÉŇťĚ×![]() ÖÖť§ĐÍşÍŇťĚ×
ÖÖť§ĐÍşÍŇťĚ×![]() ť§ĐÍץˇżËůĐč×Ę˝đˇÖąđĘÇ
ť§ĐÍץˇżËůĐč×Ę˝đˇÖąđĘÇ![]() ÍňÔŞşÍ
ÍňÔŞşÍ![]() ÍňÔŞ.ÓÚĘÇÓĐ
ÍňÔŞ.ÓÚĘÇÓĐ![]() ŁŹ˝âľĂ
ŁŹ˝âľĂ![]() .
.
ĄŕÔÚÎŁžÉˇż¸ÄÔěÖĐ˝¨łÉŇťĚ×![]() ÖÖť§ĐÍşÍŇťĚ×
ÖÖť§ĐÍşÍŇťĚ×![]() ť§ĐÍץˇżËůĐč×Ę˝đˇÖąđĘÇ45ÍňÔŞşÍ78ÍňÔŞ.
ť§ĐÍץˇżËůĐč×Ę˝đˇÖąđĘÇ45ÍňÔŞşÍ78ÍňÔŞ.
Ł¨2ŁŠ˘ŮÉ轨łÉ![]() ÖÖť§ĐÍ
ÖÖť§ĐÍ![]() ĚףŹÔň˝¨łÉ
ĚףŹÔň˝¨łÉ![]() ť§ĐÍ
ť§ĐÍ![]() ĚףŹÓÚĘÇÓĐ
ĚףŹÓÚĘÇÓĐ
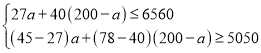 ŁŹ˝âľĂ
ŁŹ˝âľĂ![]() .
.
ĄßaÎŞŐűĘýŁŹ
Ąŕa=111ŁŹ112ŁŹ113ŁŹĄŁŹ127ŁŹ
Ąŕš˛ÓĐ17ÖָĽ¨ˇ˝°¸Łť
˘ÚÓÉĚâżÉÖŞŁş![]()
![]() .
.
Ąß![]() ŁŹĄŕ
ŁŹĄŕ![]() Ëć
Ëć![]() ľÄÔö´óśřźőĐĄ.
ľÄÔö´óśřźőĐĄ.
ÓɢٿÉÖŞ![]() ŁŹ
ŁŹ
Ąŕľą![]() ĘąŁŹ
ĘąŁŹ![]() Ł¨ÍňÔŞŁŠ.
Ł¨ÍňÔŞŁŠ.



| Äęźś | ¸ßÖĐżÎłĚ | Äęźś | łőÖĐżÎłĚ |
| ¸ßŇť | ¸ßŇťĂâˇŃżÎłĚÍĆźöŁĄ | łőŇť | łőŇťĂâˇŃżÎłĚÍĆźöŁĄ |
| ¸ßśţ | ¸ßśţĂâˇŃżÎłĚÍĆźöŁĄ | łőśţ | łőśţĂâˇŃżÎłĚÍĆźöŁĄ |
| ¸ßČý | ¸ßČýĂâˇŃżÎłĚÍĆźöŁĄ | łőČý | łőČýĂâˇŃżÎłĚÍĆźöŁĄ |
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
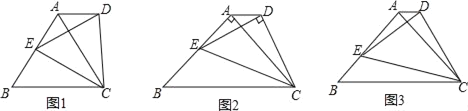
ĄžĚâÄżĄżŁ¨1ŁŠČçÍź1ÖĐŁŹĄ÷ABCÎŞŐýČý˝ÇĐÎŁŹľăEÎŞABąßÉĎČÎŇťľăŁŹŇÔCEÎŞąß×÷ŐýĄ÷DECŁŹÁŹ˝áADŁŽÇó![]() ľÄÖľŁŽ
ľÄÖľŁŽ
Ł¨2ŁŠČçÍź2ÖĐŁŹĄ÷ABCÎŞľČŃüÖą˝ÇČý˝ÇĐÎŁŹĄĎAŁ˝90ĄăŁŹľăEÎŞŃüABÉĎČÎŇâŇťľăŁŹŇÔCEÎŞĐąąß×÷ľČŃüÖą˝ÇĄ÷CDEŁŹÁŹ˝áADŁŽÇó![]() ľÄÖľŁť
ľÄÖľŁť
Ł¨3ŁŠČçÍź3ÖĐŁŹĄ÷ABCÎŞČÎŇâľČŃüČý˝ÇĐÎŁŹľăEÎŞŃüABÉĎČÎŇâŇťľăŁŹŇÔCEÎŞľ×ąß×÷ľČŃüĄ÷DECŁŹĘšĄ÷DECĄ×Ą÷ABCŁŹ˛˘ÇŇBCŁ˝![]() ACŁŽÁŹ˝áADŁŹÖą˝ÓĐ´łö
ACŁŽÁŹ˝áADŁŹÖą˝ÓĐ´łö![]() ľÄÖľŁŽ
ľÄÖľŁŽ
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżČçÍźŁŹĚÝĐÎABCDľÄśÔ˝ÇĎßACĄ˘BDĎཝÓÚOŁŹľăHÎŞBCÉĎŇťľăŁŹÁŹ˝ÓAH˝ťBDÓÚľăGŁŽČôADŁ˝3ŁŹBCŁ˝9ŁŹBHŁşHCŁ˝1Łş2ŁŹÔňGOŁşBGŁ˝Ł¨ ŁŠ
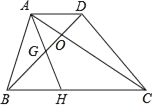
A.1Łş2B.1Łş3C.2Łş3D.11Łş20
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżČçÍźŁŹÔÚĆ˝ĂćÖą˝Ç×řąęĎľxOyÖĐŁŹÖąĎßyŁ˝![]() xžšýľăAŁŹ×÷ABĄÍxÖáÓÚľăBŁŹ˝ŤĄ÷ABOČĆľăBÄćĘąŐëĐýת60ĄăŁŹľĂľ˝Ą÷CBDŁŹČôľăBľÄ×řąęÎŞŁ¨4ŁŹ0ŁŠŁŹÔňľăCľÄ×řąęÎŞŁ¨ĄĄĄĄŁŠ
xžšýľăAŁŹ×÷ABĄÍxÖáÓÚľăBŁŹ˝ŤĄ÷ABOČĆľăBÄćĘąŐëĐýת60ĄăŁŹľĂľ˝Ą÷CBDŁŹČôľăBľÄ×řąęÎŞŁ¨4ŁŹ0ŁŠŁŹÔňľăCľÄ×řąęÎŞŁ¨ĄĄĄĄŁŠ
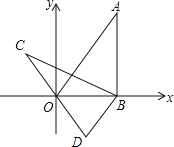
A.Ł¨Š2ŁŹ2![]() ŁŠB.Ł¨Š4ŁŹ2
ŁŠB.Ł¨Š4ŁŹ2![]() ŁŠC.Ł¨Š2
ŁŠC.Ł¨Š2![]() ŁŹ2ŁŠD.Ł¨Š2
ŁŹ2ŁŠD.Ł¨Š2![]() ŁŹ4ŁŠ
ŁŹ4ŁŠ
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżŇŃÖŞľăPĘÇRtĄ÷ABCĐąąßABËůÔÚÖąĎßÉĎľÄŇť¸ö˛ťÓëAĄ˘BÖغϾĜŻľăŁŹˇÖąđšýAĄ˘BĎňÖąĎßCP×÷´šĎߣŹ´š×ăˇÖąđÎŞEĄ˘FŁŹľăQÎŞĐąąßABľÄÖĐľă
Ł¨1ŁŠľąľăPÓëľăQÖŘşĎĘąŁŹAEÓëBFľÄÎťÖĂšŘĎľĘÇĄĄ ŁŹQEÓëQFľÄĘýÁżšŘĎľĘÇĄĄ ŁŹ˛˘ËľĂ÷ŔíÓÉŁť
Ł¨2ŁŠľąľăP˛ťÓëľăQÖŘşĎĘąŁŹĹĐśĎQEÓëQFľÄĘýÁżšŘĎľ˛˘¸řÓčÖ¤Ă÷ŁŽ
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżľçĆ÷רӪľęľÄžÓŞŔűČóĘÜľŘŔíÎťÖĂĄ˘šËżÍĎűˇŃÄÜÁŚľČŇňËŘľÄÓ°Ď죏ijơĹĆľçÄÔרӪľęÉčÓПץ˘ŇŇÁ˝źŇˇÖľęŁŹžůĎúĘŰAĄ˘BĄ˘CĄ˘DËÄÖÖżîĘ˝ľÄľçÄÔŁŹĂżÖÖżîĘ˝ľçÄÔľÄŔűČóČçąí1ËůĘžŁŽĎִӟץ˘ŇŇÁ˝ľęĂżÔÂĘŰłöľÄľçÄÔÖи÷ËćťúłéČĄËůźÇÂźľÄ50̨ľçÄԾĿîĘ˝ŁŹÍłźĆ¸÷ÖÖżîĘ˝ľçÄÔľÄĎúĘŰĘýÁżŁŹČçąí2ËůĘžŁŽ
ąí1ŁşËÄÖÖżîĘ˝ľçÄÔľÄŔűČó
ľçÄÔżîĘ˝ | A | B | C | D |
ŔűČóŁ¨ÔŞ/̨ŁŠ | 160 | 200 | 240 | 320 |
ąí2Łşź×Ą˘ŇŇÁ˝ľęľçÄÔĎúĘŰÇéżö
ľçÄÔżîĘ˝ | A | B | C | D |
ź×ľęĎúĘŰĘýÁżŁ¨Ě¨ŁŠ | 20 | 15 | 10 | 5 |
ŇŇľęĎúĘŰĘýÁżŁ¨Ě¨ŁŠ8 | 8 | 10 | 14 | 18 |
ĘÔÔËÓĂÍłźĆÓë¸ĹÂĘÖŞĘśŁŹ˝âžöĎÂÁĐÎĘĚ⣺
Ł¨1ŁŠ´Óź×ľęĂżÔÂĘŰłöľÄľçÄÔÖĐËćťúłéȥҝ̨ŁŹĆäŔűČó˛ťÉŮÓÚ240ÔŞľÄ¸ĹÂĘÎŞĄĄ ĄĄŁť
Ł¨2ŁŠžĘĐłĄľ÷˛éˇ˘ĎÖŁŹź×Ą˘ŇŇÁ˝ľęĂżÔÂľçÄÔľÄ×ÜĎúÁżĎŕľąŁŽĎÖÓÉÓÚ×Ę˝đĎŢÖĆŁŹĐčśÔĆäÖĐŇťźŇˇÖľę×÷łöÔÝÍŁÓŞŇľľÄžöś¨ŁŹČô´Óÿ̨ľçÄÔľÄĆ˝žůŔűČóľÄ˝ÇśČżźÂÇŁŹÄăČĎÎŞÓŚśÔÄğҡ־ę×÷łöÔÝÍŁÓŞŇľľÄžöś¨Łż˛˘ËľĂ÷ŔíÓÉŁŽ
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
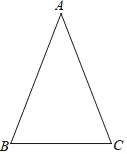
ĄžĚâÄżĄżÔÚĄ÷ABCÖĐŁŹABŁ˝AC
Ł¨1ŁŠŔűÓĂÖąłßşÍÔ˛šćÍęłÉČçĎ²Ů×÷ŁŹ×÷ĄĎBACľÄĆ˝ˇÖĎßşÍABľÄ´šÖąĆ˝ˇÖĎߣŹ˝ťľăÎŞPŁ¨˛ťĐ´×÷ˇ¨ŁŹąŁÁô×÷ÍźđýźŁŁŠ
Ł¨2ŁŠÁŹ˝áPBŁŹČôĄĎABCŁ˝65ĄăŁŹÇóĄĎABPľÄśČĘýŁŽ
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
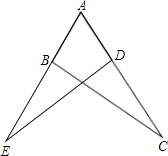
ĄžĚâÄżĄżČçÍźŁŹľăBÔÚAEÉĎŁŹľăDÔÚACÉĎŁŹAB=ADŁŽÇëÄăĚíźÓŇť¸öĘĘľąľÄĚőźţŁŹĘšĄ÷ABCĄŐĄ÷ADEŁ¨ÖťÄÜĚíźÓŇť¸öŁŠŁŽ
Ł¨1ŁŠÄăĚíźÓľÄĚőźţĘÇĄĄ ĄĄŁŽ
Ł¨2ŁŠĚíźÓĚőźţşóŁŹÇëËľĂ÷Ą÷ABCĄŐĄ÷ADEľÄŔíÓÉŁŽ
˛éż´´đ°¸şÍ˝âÎö>>
żĆÄżŁşłőÖĐĘýѧ Ŕ´Ô´Łş ĚâĐÍŁş
ĄžĚâÄżĄżŁ¨2011É˝śŤźĂÄĎŁŹ27ŁŹ9ˇÖŁŠČçÍźŁŹžŘĐÎOABCÖĐŁŹľăOΪԾ㣏ľăAľÄ×řąęÎŞŁ¨0ŁŹ8ŁŠŁŹľăCľÄ×řąęÎŞŁ¨6ŁŹ0ŁŠŁŽĹ×ÎďĎß![]() žšýAĄ˘CÁ˝ľăŁŹÓëABąß˝ťÓÚľăDŁŽ
žšýAĄ˘CÁ˝ľăŁŹÓëABąß˝ťÓÚľăDŁŽ
Ł¨1ŁŠÇóĹ×ÎďĎ߾ĺŻĘýąí´ďĘ˝Łť
Ł¨2ŁŠľăPÎŞĎßśÎBCÉĎŇť¸öśŻľăŁ¨˛ťÓëľăCÖغϣŠŁŹľăQÎŞĎßśÎACÉĎŇť¸öśŻľăŁŹAQ=CPŁŹÁŹ˝ÓPQŁŹÉčCP=mŁŹĄ÷CPQľÄĂćťýÎŞSŁŽ
˘ŮÇóSšŘÓÚmľÄşŻĘýąí´ďĘ˝ŁŹ˛˘ÇółömÎŞşÎ־ʹŁŹSČĄľĂ×î´óÖľŁť
˘ÚľąS×î´óĘąŁŹÔÚĹ×ÎďĎß![]() ľÄśÔłĆÖálÉĎČô´ćÔÚľăFŁŹĘšĄ÷FDQÎŞÖą˝ÇČý˝ÇĐÎŁŹÇëÖą˝ÓĐ´łöËůÓСűşĎĚőźţľÄFľÄ×řąęŁťČô˛ť´ćÔÚŁŹÇëËľĂ÷ŔíÓÉŁŽ
ľÄśÔłĆÖálÉĎČô´ćÔÚľăFŁŹĘšĄ÷FDQÎŞÖą˝ÇČý˝ÇĐÎŁŹÇëÖą˝ÓĐ´łöËůÓСűşĎĚőźţľÄFľÄ×řąęŁťČô˛ť´ćÔÚŁŹÇëËľĂ÷ŔíÓÉŁŽ
˛éż´´đ°¸şÍ˝âÎö>>
šúźĘѧУÓĹŃĄ - ÁˇĎ°˛áÁĐąí - ĘÔĚâÁĐąí
şţąąĘĄťĽÁŞÍřÎĽˇ¨şÍ˛ťÁźĐĹϢžŮą¨Ć˝Ě¨ | ÍřÉĎÓĐşŚĐĹϢžŮą¨×¨Çř | ľçĐĹՊƞٹ¨×¨Çř | ÉćŔúʡĐéÎŢÖ÷ŇĺÓĐşŚĐĹϢžŮą¨×¨Çř | ÉćĆóÇÖȨžŮą¨×¨Çř
ÎĽˇ¨şÍ˛ťÁźĐĹϢžŮą¨ľçť°Łş027-86699610 žŮą¨ÓĘĎ䣺58377363@163.com