
【题目】已知点P是Rt△ABC斜边AB所在直线上的一个不与A、B重合的动点,分别过A、B向直线CP作垂线,垂足分别为E、F,点Q为斜边AB的中点
(1)当点P与点Q重合时,AE与BF的位置关系是 ,QE与QF的数量关系是 ,并说明理由;
(2)当点P不与点Q重合时,判断QE与QF的数量关系并给予证明.
【答案】(1)AE∥BF, QE=QF,理由见解析;(2)①当点P在线段AB上不与点Q重合时,QE=QF,证明见解析;②当点P在线段BA(或AB)的延长线上时,结论QE=QF成立,证明见解析.
【解析】
(1)根据AAS推出△AEQ≌△BFQ,推出AE=BF即可;
(2)延长EQ交BF于D,求出△AEQ≌△BDQ,根据全等三角形的性质得出EQ=QD,根据直角三角形斜边上中点性质得出即可;延长EQ交FB于D,求出△AEQ≌△BDQ,根据全等三角形的性质得出EQ=QD,根据直角三角形斜边上中点性质得出即可.
解:(1)如图1,
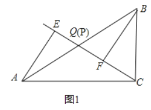
当点P与点Q重合时,AE与BF的位置关系是AE∥BF,QE与QF的数量关系是QE=QF,
理由是:∵Q为AB的中点,∴AQ=BQ,
∵AE⊥CQ,BF⊥CQ,∴AE∥BF,∠AEQ=∠BFQ=90°,
∴△AEQ≌△BFQ(AAS),
∴QE=QF,
故答案为:AE∥BF,QE=QF;
(2)①当点P在线段AB上不与点Q重合时,QE=QF,
证明:延长EQ交BF于D,如图2,

∵由(1)知:AE∥BF,
∴∠AEQ=∠BDQ,又∠AQE=∠BQD,AQ=BQ,
∴△AEQ≌△BDQ(AAS),
∴EQ=DQ,
∵∠BFE=90°,
∴QE=QF;
②当点P在线段BA(或AB)的延长线上时,此时(2)中的结论成立,
证明:延长EQ交FB于D,如图3,
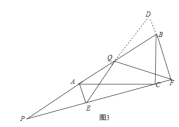
∵由(1)知:AE∥BF,
∴∠AEQ=∠BDQ,
又,∠AQE=∠BQD,AQ=BQ,
∴△AEQ≌△BDQ(AAS),
∴EQ=DQ,
∵∠BFE=90°,
∴QE=QF.


科目:初中数学 来源: 题型:
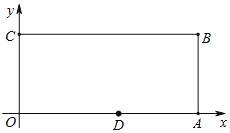
【题目】如图,已知在平面直角坐标系中,O为坐标原点,四边形OABC是长方形,点A、C、D的坐标分别为A(9,0)、C(0,4),D(5,0),点P从点O出发,以每秒1个单位长度的速度沿O→C→B→A运动,点P的运动时间为t秒.则当t=____秒时,△ODP是腰长为5的等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
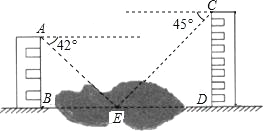
【题目】如图,两幢建筑物AB和CD,AB⊥BD,CD⊥BD,AB=15m,CD=20m.AB和CD之间有一景观池,小双在A点测得池中喷泉处E点的俯角为42°,在C点测得E点的俯角为45°,点B、E、D在同一直线上.求两幢建筑物之间的距离BD.(结果精确到0.1m)(参考数据:sin42°=0.67,cos42°=0.74,tan42°=0.90)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以坐标原点O为圆心,2为半径画圆,P是⊙O上一动点且在第一象限内,过点P作⊙O的切线,与x、y轴分别交于点A、B.
(1)求证:△OBP与△OPA相似;
(2)当点P为AB中点时,求出P点坐标;
(3)在⊙O上是否存在一点Q,使得以Q,O,A、P为顶点的四边形是平行四边形.若存在,试求出Q点坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,⊙M的半径为2,圆心M的坐标为(3,4),点P是⊙M上的任意一点,PA⊥PB,且PA、PB与x轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最小值为( )
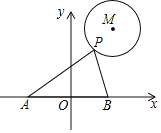
A. 3B. 4C. 6D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在实施“棚户区”改造工程中,我市计划推出![]() 、
、![]() 两种新户型.根据预算,建成10套
两种新户型.根据预算,建成10套![]() 种户型和30套
种户型和30套![]() 种户型住房共需资金2790万元,建成30套
种户型住房共需资金2790万元,建成30套![]() 种户型和10套
种户型和10套![]() 种户型住房共需资金2130万元.
种户型住房共需资金2130万元.
(1)在危旧房改造中建成一套![]() 种户型和一套
种户型和一套![]() 种户型住房所需资金分别是多少万元?
种户型住房所需资金分别是多少万元?
(2)河西区有200套住房需要改造,改造资金由国家危旧房补贴和地方财政共同承担,若国家危旧房补贴拨付的改造资金不超过6560万元,地方财政投入额资金不少于5050万元,其中国家危旧房补贴投入到![]() 、
、![]() 两种户型的改造资金分别为每套27万元和40万元
两种户型的改造资金分别为每套27万元和40万元
①请你设计出改造方案:
②设这项改造工程总投入资金![]() 万元,建成
万元,建成![]() 种户型
种户型![]() 套,写出
套,写出![]() 与
与![]() 的关系式,并求出最少总投入.
的关系式,并求出最少总投入.
查看答案和解析>>
科目:初中数学 来源: 题型:
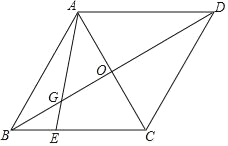
【题目】如图,在菱形ABCD中,点E是BC边上一动点(不与点C重合)对角线AC与BD相交于点O,连接AE,交BD于点G.
(1)根据给出的△AEC,作出它的外接圆⊙F,并标出圆心F(不写作法和证明,保留作图痕迹);
(2)在(1)的条件下,连接EF.①求证:∠AEF=∠DBC;
②记t=GF2+AGGE,当AB=6,BD=6![]() 时,求t的取值范围.
时,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017·吉林)如图①,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,28s时注满水槽.水槽内水面的高度y(cm)与注水时间x(s)之间的函数图象如图②所示.
(1)正方体的棱长为 cm;
(2)求线段AB对应的函数解析式,并写出自变量x的取值范围;
(3)如果将正方体铁块取出,又经过t(s)恰好将此水槽注满,直接写出t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
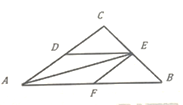
【题目】如图,在△ABC中,AB=3+![]() ,∠B=45°,∠C=105°,点 D、E、F分别在AC、BC、AB上,且四边形ADEF为菱形,若点P是AE上一个动点,则PF+PB的最小值为___________ 。
,∠B=45°,∠C=105°,点 D、E、F分别在AC、BC、AB上,且四边形ADEF为菱形,若点P是AE上一个动点,则PF+PB的最小值为___________ 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com