
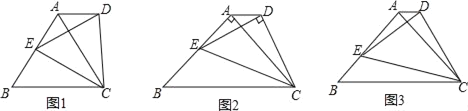
【题目】(1)如图1中,△ABC为正三角形,点E为AB边上任一点,以CE为边作正△DEC,连结AD.求![]() 的值.
的值.
(2)如图2中,△ABC为等腰直角三角形,∠A=90°,点E为腰AB上任意一点,以CE为斜边作等腰直角△CDE,连结AD.求![]() 的值;
的值;
(3)如图3中,△ABC为任意等腰三角形,点E为腰AB上任意一点,以CE为底边作等腰△DEC,使△DEC∽△ABC,并且BC=![]() AC.连结AD,直接写出
AC.连结AD,直接写出![]() 的值.
的值.
【答案】(1)1;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由三角形ABC与三角形CDE都为正三角形,得到AB=AC,CE=CD,以及内角为60°,利用等式的性质得到∠ECB=∠DCA,利用SAS得到三角形ECB与三角形DCA全等,利用全等三角形对应边相等得到BE=AD,即可求出所求之比;
(2)由三角形CDE与三角形ABC都为等腰直角三角形,利用等腰直角三角形的性质得到CE=![]() CD,BC=
CD,BC=![]() AC,以及锐角为45°,利用等式的性质得到∠ECB=∠DCA,利用两边对应成比例且夹角相等的三角形相似得到三角形ECB与三角形DCA相似,利用相似三角形对应边成比例即可求出所求之比;
AC,以及锐角为45°,利用等式的性质得到∠ECB=∠DCA,利用两边对应成比例且夹角相等的三角形相似得到三角形ECB与三角形DCA相似,利用相似三角形对应边成比例即可求出所求之比;
(3)仿照前两问,以此类推得到一般性规律,求出所求之比即可.
解:(1)∵△ABC和△CDE都是正三角形,
∴∠B=∠ACB=∠DCE=60°,AB=AC,CE=DC,
∵∠ECB=∠ACB﹣∠ACE=60°﹣∠ACE,
∠DCA=∠DCE﹣∠ACE=60°﹣∠ACE,
∴∠ECB=∠DCA,
在△ECB和△DCA中,
 ,
,
∴△ECB≌△DCA(SAS),
∴BE=AD,
则![]() =1;
=1;
(2)∵等腰Rt△ABC和等腰Rt△CDE中,
∴∠B=∠ACB=∠DCE=45°,CE=![]() DC,BC=
DC,BC=![]() AC,
AC,
∴![]() ,
,
∵∠ECB=∠ACB﹣∠ACE=45°﹣∠ACE,
∠ACD=∠DCE﹣∠ACE=45°﹣∠ACE,
∴∠ECB=∠DCA,
∴△ECB∽△DCA,
∴![]() ;
;
(3)依此类推,当BC=![]() AC时,
AC时,![]() =
=![]() ,理由为:
,理由为:
∵等腰△ABC和等腰△CDE中,
∴∠B=∠ACB=∠DCE,CE=![]() DC,BC=
DC,BC=![]() AC,
AC,
∴![]() ,
,
∵∠ECB=∠ACB﹣∠ACE,∠ACD=∠DCE﹣∠ACE,
∴∠ECB=∠DCA,
∴△ECB∽△DCA,
∴![]() =
=![]() .
.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉,经市场调查,甲种花卉的种植费用y(元)与种植面积x(m2)之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
(1)直接写出当0≤x≤300和x>300时,y与x的函数关系式;
(2)广场上甲、乙两种花卉的种植面积共1200m2,若甲种花卉的种植面积不少于200m2,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植总费用最少?最少总费用为多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
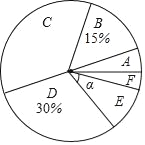
【题目】在星期一的第八节课,我校体育老师随机抽取了九年级的总分学生进行体育中考的模拟测试,并对成绩进行统计分析,绘制了频数分布表和统计图,按得分划分成A、B、C、D、E、F六个等级,并绘制成如下两幅不完整的统计图表.
等级 | 得分x(分) | 频数(人) |
A | 95<x≤100 | 4 |
B | 90<x≤95 | m |
C | 85<x≤90 | n |
D | 80<x≤85 | 24 |
E | 75<x≤80 | 8 |
F | 70<x≤75 | 4 |
请你根据图表中的信息完成下列问题:
1)本次抽样调查的样本容量是 .其中m= ,n= .
2)扇形统计图中,求E等级对应扇形的圆心角α的度数;
3)我校九年级共有700名学生,估计体育测试成绩在A、B两个等级的人数共有多少人?
4)我校决定从本次抽取的A等级学生(记为甲、乙、丙、丁)中,随机选择2名成为学校代表参加全市体能竞赛,请你用列表法或画树状图的方法,求恰好抽到甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
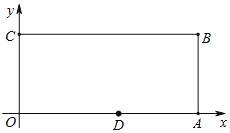
【题目】如图,已知在平面直角坐标系中,O为坐标原点,四边形OABC是长方形,点A、C、D的坐标分别为A(9,0)、C(0,4),D(5,0),点P从点O出发,以每秒1个单位长度的速度沿O→C→B→A运动,点P的运动时间为t秒.则当t=____秒时,△ODP是腰长为5的等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC=5,BC=8,D,E分别为BC,AB边上一点,∠ADE=∠C.
(1)求证:△BDE∽△CAD;
(2)若CD=2,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=6,AD=8,点E是边AD上一点,EM⊥BC交AB于点M,点N在射线MB上,且AE是AM和AN的比例中项.
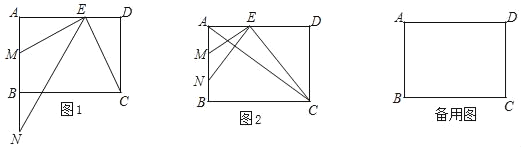
(1)如图1,求证:∠ANE=∠DCE;
(2)如图2,当点N在线段MB之间,联结AC,且AC与NE互相垂直,求MN的长;
(3)连接AC,如果△AEC与以点E、M、N为顶点所组成的三角形相似,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B处的求救者后,又发现点B正上方点C处还有一名求救者.在消防车上点A处测得点B和点C的仰角分别是45°和65°,点A距地面2.5米,点B距地面10.5米.为救出点C处的求救者,云梯需要继续上升的高度BC约为多少米?(结果保留整数.参考数据:tan65°≈2.1,sin65°≈0.9,cos65°≈0.4,![]() ≈1.4)
≈1.4)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在实施“棚户区”改造工程中,我市计划推出![]() 、
、![]() 两种新户型.根据预算,建成10套
两种新户型.根据预算,建成10套![]() 种户型和30套
种户型和30套![]() 种户型住房共需资金2790万元,建成30套
种户型住房共需资金2790万元,建成30套![]() 种户型和10套
种户型和10套![]() 种户型住房共需资金2130万元.
种户型住房共需资金2130万元.
(1)在危旧房改造中建成一套![]() 种户型和一套
种户型和一套![]() 种户型住房所需资金分别是多少万元?
种户型住房所需资金分别是多少万元?
(2)河西区有200套住房需要改造,改造资金由国家危旧房补贴和地方财政共同承担,若国家危旧房补贴拨付的改造资金不超过6560万元,地方财政投入额资金不少于5050万元,其中国家危旧房补贴投入到![]() 、
、![]() 两种户型的改造资金分别为每套27万元和40万元
两种户型的改造资金分别为每套27万元和40万元
①请你设计出改造方案:
②设这项改造工程总投入资金![]() 万元,建成
万元,建成![]() 种户型
种户型![]() 套,写出
套,写出![]() 与
与![]() 的关系式,并求出最少总投入.
的关系式,并求出最少总投入.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com