
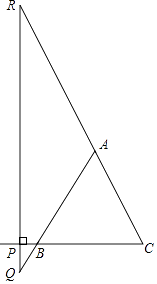
【题目】如图(1),点P是等腰三角形ABC底边BC上的一动点,过点P作BC的垂线,交直线AB于点Q,交CA的延长线于点R. 
(1)请观察AR与AQ,它们相等吗?并证明你的猜想.
(2)如图(2)如果点P沿着底边BC所在的直线,按由C向B的方向运动到CB的延长线上时,(1)中所得的结论还成立吗?请你在图(2)中完成图形,并给予证明. 
【答案】
(1)解:AR=AQ.
理由如下:∵△ABC是等腰三角形,
∴AB=AC,
∴∠B=∠C,
∵PR⊥BC,
∴∠B+∠BQP=90°,
∠C+∠PRC=90°,
∴∠BQP=∠PRC,
∵∠BQP=∠AQR(对顶角相等),
∴∠AQR=∠PRC,
∴AR=AQ
(2)AR=AQ依然成立.
理由如下:如图,∵△ABC是等腰三角形,
∴AB=AC,
∴∠ABC=∠C,
∵∠ABC=∠PBQ(对顶角相等),
∴∠C=∠PBQ,
∵PR⊥BC,
∴∠R+∠C=90°,
∠Q+∠PBQ=90°,
∴∠Q=∠R,
∴AR=AQ.
【解析】(1)根据等腰三角形的性质求出∠B=∠C,根据等角的余角相等求出∠BQP=∠PRC,再根据对顶角相等可得∠BQP=∠AQR,从而得到∠AQR=∠PRC,然后根据等角对等边证明即可;(2)根据等腰三角形的性质求出∠ABC=∠C,再根据对顶角相等可得∠ABC=∠PBQ,从而得到∠C=∠PBQ,然后根据等角的余角相等求出∠Q=∠R,最后根据等角对等边证明即可.
【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识,掌握等腰三角形的两个底角相等(简称:等边对等角).


科目:初中数学 来源: 题型:
【题目】老师在黑板上出了一道解方程的题 ![]() =1﹣
=1﹣ ![]() ,小明马上举起了手,要求到黑板上去做,他是这样做的:
,小明马上举起了手,要求到黑板上去做,他是这样做的:
4(2x﹣1)=1﹣3(x+2)①
8x﹣4=1﹣3x﹣6 ②
8x+3x=1﹣6+4 ③
11x=﹣1 ④![]() ⑤
⑤
老师说:小明解一元一次方程的一般步骤都掌握了,但解题时有一步做错了,请你指出他错在第步(填编号),错误的原因是;然后,你自己细心地解下列方程: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD. 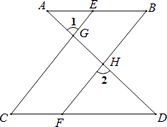
理由如下:
∵∠1=∠2(已知),
且∠1=∠CGD()
∴∠2=∠CGD(等量代换)
∴CE∥BF()
∴∠=∠BFD()
又∵∠B=∠C(已 知)
∴(等量代换)
∴AB∥CD()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,把一张长方形的纸片ABCD沿对角线BD折叠,点C落在E处,BE交AD于点F. 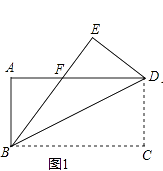
(1)求证:FB=FD;
(2)如图2,连接AE,求证:AE∥BD; 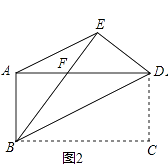
(3)如图3,延长BA,DE相交于点G,连接GF并延长交BD于点H,求证:GH垂直平分BD. 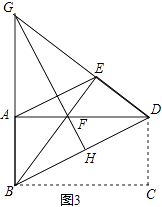
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件40元,如果售价为每件50元,每个月可卖出210件;如果售价超过50元,每上涨1元,则每个月少卖3件.设每件商品的售价为x元,每个月的销售量为y件.
(1)求y与x的函数关系式并直接写出自变量x的取值范围;
(2)设每月的销售利润为W,请直接写出W与x的函数关系式;
(3)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
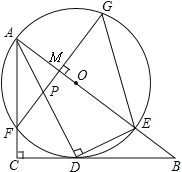
【题目】如图,在Rt△ABC中,∠C=90°,AD是角平分线,DE⊥AD交AB于E,△ADE的外接圆⊙O与边AC相交于点F,过F作AB的垂线交AD于P,交AB于M,交⊙O于G,连接GE.
(1)求证:BC是⊙O的切线;
(2)若tan∠G=![]() ,BE=4,求⊙O的半径;
,BE=4,求⊙O的半径;
(3)在(2)的条件下,求AP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com