
【题目】如图,在Rt△ABC中,∠C=90°,AD是角平分线,DE⊥AD交AB于E,△ADE的外接圆⊙O与边AC相交于点F,过F作AB的垂线交AD于P,交AB于M,交⊙O于G,连接GE.
(1)求证:BC是⊙O的切线;
(2)若tan∠G=![]() ,BE=4,求⊙O的半径;
,BE=4,求⊙O的半径;
(3)在(2)的条件下,求AP的长.
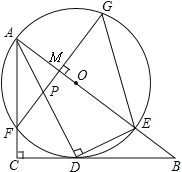
【答案】(1)证明见解析;(2)6;(3)![]()
【解析】试题分析:(1)连结OD,根据AD是角平分线,求出∠C=90°,得到OD⊥BC,求出BC是⊙O的切线;
(2)构造直角三角形,根据勾股定理求出k的值即可;
(3)设FG与AE的交点为M,连结AG,利用三角函数和相似三角形结合勾股定理解题.
试题解析:(1)证明:连结OD.∵DE⊥AD,∴AE是⊙O的直径,即O在AE上.
∵AD是角平分线,∴∠1=∠2.
∵OA=OD,∴∠2=∠3.∴∠1=∠3.∴OD∥AC.
∵∠C=90°,∴OD⊥BC.∴BC是⊙O的切线.
(2)解:∵OD∥AC,∴∠4=∠EAF.
∵∠G=∠EAF,∴∠4=∠G.
∴tan∠4=tan∠G=![]() .
.
设BD=4k,则OD=OE=3k.
在Rt△OBD中,由勾股定理得(3k)2+(4k)2=(3k+4)2,
解得,k1=2,k2=![]() (舍),(注:也可由OB=5k=3k+4得k=2),
(舍),(注:也可由OB=5k=3k+4得k=2),
∴3k=6,即⊙O的半径为6.
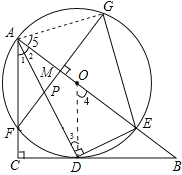
(3)解:连结AG,则∠AGE=90°,∠EGM=∠5.
∴tan∠5=tan∠EGM=![]() ,即
,即![]() ,
, ![]() ,
,
∴![]() ,
,
∴AM=![]() AE=
AE=![]() =
=![]() .
.
∵OD∥AC,∴![]() ,
, ![]() ,即
,即![]() ,
, ![]() .
.
∴AC=![]() ,CD=
,CD=![]() .
.
∵∠1=∠2,∠ACD=∠AMP=90°,∴△ACD∽△AMP.
∴![]() ,∴PM=
,∴PM= ![]() =
=![]() .
.
∴AP=![]() =
=![]() .
.


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
【题目】如图(1),点P是等腰三角形ABC底边BC上的一动点,过点P作BC的垂线,交直线AB于点Q,交CA的延长线于点R. 
(1)请观察AR与AQ,它们相等吗?并证明你的猜想.
(2)如图(2)如果点P沿着底边BC所在的直线,按由C向B的方向运动到CB的延长线上时,(1)中所得的结论还成立吗?请你在图(2)中完成图形,并给予证明. 
查看答案和解析>>
科目:初中数学 来源: 题型:
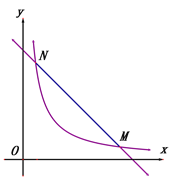
【题目】已知直线![]() (k>0)与双曲线
(k>0)与双曲线![]() (x>0)交于点M、N,且点N的横坐标为k. .
(x>0)交于点M、N,且点N的横坐标为k. .
(1) 如图1,当k=1时.
①求m的值及线段MN的长;
②在y轴上是否是否存在点Q,使∠MQN=90°,若存在,请求出点Q的坐标;若不存在,请说明理由.
(2) 如图2,以MN为直径作⊙P,当⊙P与y轴相切时,求k值.
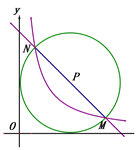
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,BC=DC,AC、BD相交于点O,点E在AO上,且OE=OC.
(1)求证:∠1=∠2;
(2)连结BE、DE,判断四边形BCDE的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将抛物线y=﹣2(x﹣1)2+3向下平移2个单位后所得抛物线的表达式为( )
A. y=﹣2(x+1)2+3B. y=﹣2(x﹣3)2+3
C. y=﹣2(x﹣1)2+5D. y=﹣2(x﹣1)2+1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在读书月活动中,某校号召全体师生积极捐书,为了解所捐书籍的种类,图书管理员对部分书籍进行了抽样调查,根据调查数据绘制了如下不完整的统计图表.请你根据统计图表所提供的信息回答下面问题:
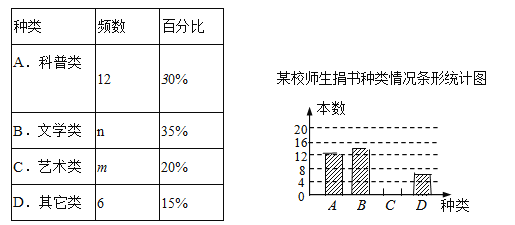
(1)统计表中的n= ______,并补全条形统计图;
(2)本次活动师生共捐书2000本,请估计有多少本科普类图书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,对角线AC⊥BD,且AC=2,BD=2,各边 中点分别为A1、B1、C1、D1,顺次连接得到四边形A1B1C1D1,再取各边中点A2、B2、C2、D2,顺次连接得到四边形A2B2C2D2,…,依此类推,这样得到四边形AnBnCnDn,则四边形AnBnCnDn的面积为_________

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com