
【题目】将一张矩形纸条ABCD按如图所示折叠,若折叠角∠FEC=64°. 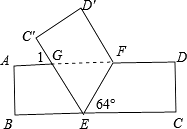
(1)求∠1的度数;
(2)求证:△EFG是等腰三角形.
【答案】
(1)解:∵∠GEF=∠FEC=64°,
∴∠BEG=180°﹣64°×2=52°
∵AD∥BC,
∴∠1=∠BEG=52°
(2)证明:∵AD∥BC,
∴∠GFE=∠FEC
∴∠GEF=∠GFE
∴GE=GF,
∴△EFG是等腰三角形
【解析】(1)根据翻折变换的性质求出∠GEF的度数,从而求出∠GEB的度数,再根据平行线的性质求出∠1;(2)根据AD∥BC得到∠GFE=∠FEC,根据翻折不变性得到∠GEF=∠GFE,由等角对等边得到GE=GF.
【考点精析】根据题目的已知条件,利用翻折变换(折叠问题)的相关知识可以得到问题的答案,需要掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.


科目:初中数学 来源: 题型:
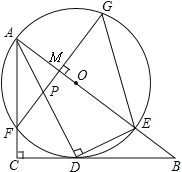
【题目】如图,在Rt△ABC中,∠C=90°,AD是角平分线,DE⊥AD交AB于E,△ADE的外接圆⊙O与边AC相交于点F,过F作AB的垂线交AD于P,交AB于M,交⊙O于G,连接GE.
(1)求证:BC是⊙O的切线;
(2)若tan∠G=![]() ,BE=4,求⊙O的半径;
,BE=4,求⊙O的半径;
(3)在(2)的条件下,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD、过点D作DE⊥AC,垂足为点E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)求证:△FDB∽△FAD;
(3)如果⊙O的半径为5,sin∠ADE=![]() ,求BF的长.
,求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E为等腰△ABC的底边BC上一动点,过E作EF⊥BC交AB于D,交CA的延长线于F,问: 
(1)∠F与∠ADF的关系怎样?说明理由;
(2)若E在BC延长线上,其余条件不变,上题的结论是否成立?若不成立,说明理由;若成立,画出图形并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,BF、DE相交于点A,BG交BF于点B,交AC于点C.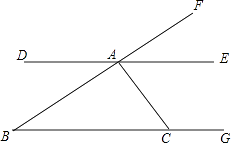
(1)指出ED、BC被BF所截的同位角,内错角,同旁内角;
(2)指出ED、BC被AC所截的内错角,同旁内角;
(3)指出FB、BC被AC所截的内错角,同旁内角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AE⊥BC于E,AE=BE,D是AE上的一点,且DE=CE,连接BD,CD.
(1)试判断BD与AC的位置关系和数量关系,并说明理由;
(2)如图2,若将△DCE绕点E旋转一定的角度后,试判断BD与AC的位置关系和数量关系是否发生变化,并说明理由;
(3)如图3,若将(2)中的等腰直角三角形都换成等边三角形,其他条件不变.
①试猜想BD与AC的数量关系,并说明理由;
②你能求出BD与AC的夹角度数吗?如果能,请直接写出夹角度数;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有两个长度相同的滑梯靠在一面墙上.已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则这两个滑梯与地面夹角∠ABC与∠DFE的度数和是( )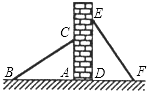
A.60°
B.90°
C.120°
D.150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,网格中的每个小正方形的边长为1,A,B是格点,则以A,B,C为等腰三角形顶点的所有格点C的位置有( )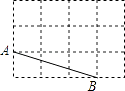
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]()
(1)A,B间的距离是;
(2)若点C也是数轴上的点,C到B的距离是C到原点O的距离的3倍,求C对应的数;
(3)若当电子P从B点出发,以6个单位长度/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4个单位长度/秒的速度向左运动,设两只电子蚂蚁在数轴上的D点相遇,那么D点对应的数是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com