Question

【题目】如图，在△ABC中，AB=AC，以AB为直径作半圆⊙O，交BC于点D，连接AD、过点D作DE⊥AC，垂足为点E，交AB的延长线于点F．

（1）求证：EF是⊙O的切线；

（2）求证：△FDB∽△FAD；

（3）如果⊙O的半径为5，sin∠ADE=，求BF的长．

Answer 1

【答案】解：（1）证明：如图，连接OD，

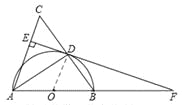
∵AB为⊙O的直径，∴∠ADB=90°。

∴AD⊥BC。

∵AB=AC，∴AD平分BC，即DB=DC。

∵OA=OB，∴OD为△ABC的中位线。

∴OD∥AC。

∵DE⊥AC，∴OD⊥DE。

∵OD是⊙O的半径，∴EF是⊙O的切线。

（2）∵∠DAC=∠DAB，∴∠ADE=∠ABD。

∴在Rt△ADB中， 。

∵AB=10，∴AD=8，

∵在Rt△ADE中， ，∴。

∵OD∥AE，∴△FDO∽△FEA。

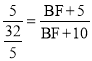∴，即，解得。

【解析】试题分析：（1）连接OD，AB为⊙0的直径得∠ADB=90°，由AB=AC，根据等腰三角形性质得AD平分BC，即DB=DC，则OD为△ABC的中位线，所以OD∥AC，而DE⊥AC，则OD⊥DE，然后根据切线的判定方法即可得到结论；

（2）利用两角对应相等的两三角形相似进行证明即可．

（3）由∠DAC=∠DAB，根据等角的余角相等得∠ADE=∠ABD，在Rt△ADB中，利用解直角三角形的方法可计算出AD=8，在Rt△ADE中可计算出AE=，然后由OD∥AE，得△FDO∽△FEA，再利用相似比可计算出BF．

试题解析：（1）证明：连接OD，如图，

∵AB为⊙0的直径，

∴∠ADB=90°，

∴AD⊥BC，

∵AB=AC，

∴AD平分BC，即DB=DC，

∵OA=OB，

∴OD为△ABC的中位线，

∴OD∥AC，

∵DE⊥AC，

∴OD⊥DE，

∴EF是⊙0的切线；

（2）证明：∵EF是⊙O的切线，

∴∠ODB+∠BDF=90°，

∵OD=OB，

∴∠OBD=∠ODB，

∴∠OBD+∠BDF=90°，

∵AB是⊙O的直径，

∴∠ADB=90°，

∴∠DAB+∠OBD=90°，

∴∠DAB=∠BDF，

∵∠BFD=∠DFA，

∴△FDB∽△FAD；

（3）∵∠DAC=∠DAB，

∴∠ADE=∠ABD，

在Rt△ADB中，sin∠ADE=sin∠ABD=，而AB=10，

∴AD=8，

在Rt△ADE中，sin∠ADE=，

∴AE=，

∵OD∥AE，

∴△FDO∽△FEA，

∴，

即，

∴BF=．