
����Ŀ����ͼ1���ڡ�ABC�У�AE��BC��E��AE=BE��D��AE�ϵ�һ�㣬��DE=CE������BD��CD��
��1�����ж�BD��AC��λ�ù�ϵ��������ϵ����˵�����ɣ�
��2����ͼ2��������DCE�Ƶ�E��תһ���ĽǶȺ����ж�BD��AC��λ�ù�ϵ��������ϵ�Ƿ����仯����˵�����ɣ�
��3����ͼ3��������2���еĵ���ֱ�������ζ����ɵȱ������Σ������������䣮
���Բ���BD��AC��������ϵ����˵�����ɣ�
���������BD��AC�ļнǶ���������ܣ���ֱ��д���нǶ�����������ܣ���˵�����ɣ�
���𰸡�
��1��
�⣺BD=AC��BD��AC��
���ɣ��ӳ�BD��AC��F��
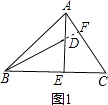
��AE��BC��
���AEB=��AEC=90�㣬
�ڡ�BED�͡�AEC�� 
���BED�ա�AEC��
��BD=AC����DBE=��CAE��
�ߡ�BED=90�㣬
���EBD+��BDE=90�㣬
�ߡ�BDE=��ADF��
���ADF+��CAE=90�㣬
���AFD=180�㩁90��=90�㣬
��BD��AC
��2��
�⣺
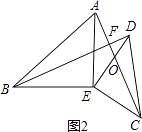
�������仯��
�����ǣ��ߡ�BEA=��DEC=90�㣬
���BEA+��AED=��DEC+��AED��
���BED=��AEC��
�ڡ�BED�͡�AEC�� 
���BED�ա�AEC��
��BD=AC����BDE=��ACE��
�ߡ�DEC=90�㣬
���ACE+��EOC=90�㣬
�ߡ�EOC=��DOF��
���BDE+��DOF=90�㣬
���DFO=180�㩁90��=90�㣬
��BD��AC
��3��
�⣺�ܣ�
���ɣ��ߡ�ABE�͡�DEC�ǵȱ������Σ�
��AE=BE��DE=EC����EDC=��DCE=60�㣬��BEA=��DEC=60�㣬
���BEA+��AED=��DEC+��AED��
���BED=��AEC��
�ڡ�BED�͡�AEC���� 
���BED�ա�AEC��
���BDE=��ACE��
���DFC=180�㩁����BDE+��EDC+��DCF��
=180�㩁����ACE+��EDC+��DCF��
=180�㩁��60��+60�㣩
=60�㣬
��BD��AC���ɵĽǵĶ���Ϊ60���120��
����������1���ӳ�BD��AC��F�������AEB=��AEC=90�㣬֤����BED�ա�AEC���Ƴ�BD=AC����DBE=��CAE�����ݡ�EBD+��BDE=90���Ƴ���ADF+��CAE=90�㣬�����AFD=90�㼴�ɣ���2�������BED=��AEC��֤����BED�ա�AEC���Ƴ�BD=AC����BDE=��ACE�����ݡ�ACE+��EOC=90�������BDE+��DOF=90�㣬�����DFO=90�㼴�ɣ���3�������BED=��AEC��֤����BED�ա�AEC���Ƴ���BDE=��ACE�������������ڽǺͶ��������DFC���ɣ�
�����㾫�������������ε��ڽǺ���Ǻ�ȫ�������ε������ǽ����ĸ�������Ҫ֪�������ε������ڽ��У�ֻ������һ���ڽ���ֱ�ǻ�۽ǣ�ֱ�������ε�������ǻ��ࣻ�����ε�һ����ǵ��ں��������ڵ������ڽǵĺͣ������ε�һ����Ǵ����κ�һ�����������ڵ��ڽǣ�ȫ�������εĶ�Ӧ�����; ȫ�������εĶ�Ӧ����ȣ�


 ���źþ���Ԫ����ĩ��ϵ�д�
���źþ���Ԫ����ĩ��ϵ�д� һ����ʦȨ����ҵ��ϵ�д�
һ����ʦȨ����ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڶ����»�У�ijУ����ȫ��ʦ���������飬Ϊ�˽������鼮�����࣬ͼ�����Ա�Բ����鼮�����˳������飬���ݵ������ݻ��������²�������ͳ��ͼ�����������ͳ��ͼ�����ṩ����Ϣ�ش��������⣺
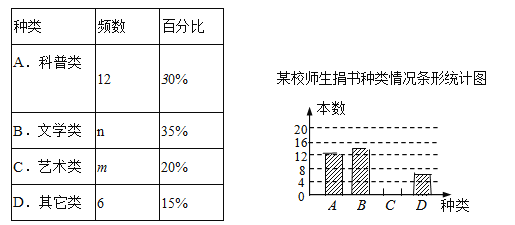
��1��ͳ�Ʊ��е�n= ______,����ȫ����ͳ��ͼ��
��2�����λʦ��������2000����������ж��ٱ�������ͼ�飿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ��MN���ABC�ı�AB��AC�ֱ���E��F����ͼ�е��ڴ����У������� 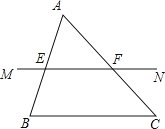
A.2��
B.4��
C.6��
D.8��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������6��˵�����١�1���4���ڴ��ǣ��ڡ�1���2��ͬλ�ǣ��ۡ�2���4���ڴ��ǣ��ܡ�4���5��ͬ���ڽǣ��ݡ�2���4��ͬλ�ǣ��ޡ�2���5���ڴ��ǣ�������ȷ���� ( ) 
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�ž���ֽ��ABCD����ͼ��ʾ�۵������۵��ǡ�FEC=64�㣮 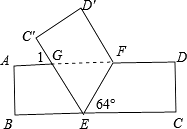
��1�����1�Ķ�����
��2����֤����EFG�ǵ��������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A��x����4�����B��3��y������x��Գƣ���ôx+y��ֵΪ��������
A.2B.��1C.7D.1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵ�У���ABC��������������ֱ�ΪA��0��4����B��3��4����C��4����1����
��1������ƽ��ֱ������ϵ�У�������ABC�� 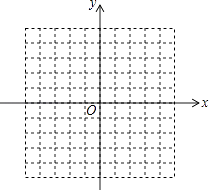
��2������A1B1C1���ABC����x��Գƣ�д��A1��B1��C1�����ꣻ
��3����x�����ҵ�һ��P��ʹ��P����A��B����ľ������С��
��4�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ֱ���У�������һ������������������ ����
A. ֱ��y= x��1 �� B. ֱ��y= ��x+1�� C. ֱ��y=x+1�� D. ֱ��y=��x��1 ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com