
【题目】如图,四边形ABCD中,对角线AC⊥BD,且AC=2,BD=2,各边 中点分别为A1、B1、C1、D1,顺次连接得到四边形A1B1C1D1,再取各边中点A2、B2、C2、D2,顺次连接得到四边形A2B2C2D2,…,依此类推,这样得到四边形AnBnCnDn,则四边形AnBnCnDn的面积为_________

【答案】![]()
【解析】根据三角形的面积公式,可以求得四边形ABCD的面积是16;根据三角形的中位线定理,得A1B1∥AC,A1B1=![]() AC,则△BA1B1∽△BAC,得△BA1B1和△BAC的面积比是相似比的平方,即
AC,则△BA1B1∽△BAC,得△BA1B1和△BAC的面积比是相似比的平方,即![]() ,因此四边形A1B1C1D1的面积是四边形ABCD的面积的
,因此四边形A1B1C1D1的面积是四边形ABCD的面积的![]() ,即a2;推而广之,则AC=2,BD=2,四边形AnBnCnDn的面积=
,即a2;推而广之,则AC=2,BD=2,四边形AnBnCnDn的面积=![]() .
.
解:∵四边形A1B1C1D1的四个顶点A1、B1、C1、D1分别为AB、BC、CD、DA的中点,
∴A1B1∥AC,A1B1=![]() AC.
AC.
∴△BA1B1∽△BAC.
∴△BA1B1和△BAC的面积比是相似比的平方,即![]() .
.
又四边形ABCD的对角线AC=2,BD=2,AC⊥BD,
∴四边形ABCD的面积是2.
推而广之,则AC=2,BD=2,四边形AnBnCnDn的面积=![]() .
.
“点睛”此题综合运用了三角形的中位线定理、相似三角形的判定及性质.注意:对角线互相垂直的四边形的面积等于对角线乘积的一半.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】△ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为 . 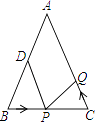
查看答案和解析>>
科目:初中数学 来源: 题型:
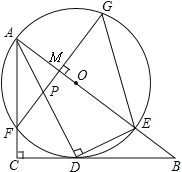
【题目】如图,在Rt△ABC中,∠C=90°,AD是角平分线,DE⊥AD交AB于E,△ADE的外接圆⊙O与边AC相交于点F,过F作AB的垂线交AD于P,交AB于M,交⊙O于G,连接GE.
(1)求证:BC是⊙O的切线;
(2)若tan∠G=![]() ,BE=4,求⊙O的半径;
,BE=4,求⊙O的半径;
(3)在(2)的条件下,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古城黄州以其名胜古迹吸引了不少游客.从地图上看,较有名的六外景点在黄州城内的分布是∶东坡赤壁在市政府以西2km再往南3km处,黄冈中学在市政府以东1 km处,宝塔公园在市政府以东3km处,鄂黄长江桥在市政府以东7 km再往北8 km处,遗爱湖在市政府以东4km再往北4km处,博物馆在市政府以北2 km再往西1 km处。请画图表示出这六个景点的位置,并用坐标表示出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD、过点D作DE⊥AC,垂足为点E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)求证:△FDB∽△FAD;
(3)如果⊙O的半径为5,sin∠ADE=![]() ,求BF的长.
,求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有两个长度相同的滑梯靠在一面墙上.已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则这两个滑梯与地面夹角∠ABC与∠DFE的度数和是( )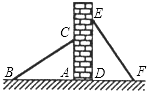
A.60°
B.90°
C.120°
D.150°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com