Question

【题目】如图，已知AD∥CB，∠1＝∠2，∠BAE＝∠DCF。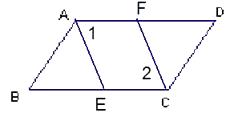

试说明：
（1）AE∥CF；
（2）AB∥CD。

Answer 1

【答案】
（1）解：∵AD∥CB （已知）
∴ ∠1=∠AEB （两直线平行，内错角相等）
又∵∠1＝∠2（已知）
∴ ∠AEB= ∠2（等量代换）
∴AE∥CF（同位角相等，两直线平行）
（2）解：∵三角形ABE的内角和是180 ∴∠B+∠BAE+∠AEB=180
又∵∠AEB= ∠2（已证） ∠BAE＝∠DCF（已知）
∴∠B+∠2+∠DCF=180 即∠B+∠BCD=180
∴AB∥CD（同旁内角互补，两直线平行）
【解析】（1）根据平行线的性质两直线平行，内错角相等得出∠1=∠AEB ，根据等量代换得出∠AEB= ∠2 ，根据平行线的判断同位角相等，两直线平行得出AE∥CF ；
（2）根据三角形的内角和得出∠B+∠BAE+∠AEB=180 ，又∠AEB= ∠2 ， ∠BAE＝∠DCF ，利用等量代换得出∠B+∠2+∠DCF=180 ， 即∠B+∠BCD=180 ，根据平行线的判断同旁内角互补，两直线平行得出AB∥CD 。