
在Rt△ABC中,∠C=90,AC=4cm,BC=3cm,则以2.4cm为半径的⊙C与直线AB的关系是 .
相切 .
【考点】直线与圆的位置关系.
【分析】过C作CD⊥AB于D,根据勾股定理求出AB,根据三角形的面积公式求出CD,最后根据直线和圆的位置关系得出即可.
【解答】解:相切,理由是:
过C作CD⊥AB于D,
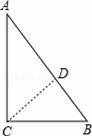

∵在Rt△ABC中,∠C=90,AC=4cm,BC=3cm,
∴由勾股定理得:AB=5cm,
∵由三角形的面积公式得:
 AC×BC=
AC×BC=
 AB×CD,
AB×CD,
∴3×4=5CD,
∴CD=2.4cm,
∴以2.4cm为半径的⊙C与直线AB的关系是相切,
故答案为:相切.
【点评】本题考查了勾股定理,三角形的面积,直线和圆的位置关系的应用,解此题的关键是能正确作出辅助线,并进一步求出CD的长,注意:直线和圆的位置关系有:相离,相切,相交.


科目:初中数学 来源: 题型:
为了估计某市空气质量情况,某同学在30天里做了如下记录:
| 污染指数(w) | 40 | 60 | 80 | 100 | 120 | 140 |
| 天数(天) | 3 | 5 | 10 | 6 | 5 | 1 |
其中w<50时空气质量为优,50≤w≤100时空气质量为良,100<w≤150时空气质量为轻度污染,若1年按365天计算,请你估计该城市在一年中空气质量达到良以上(含良)的天数为 天.
查看答案和解析>>
科目:初中数学 来源: 题型:
把一副三角板的直角顶点O重叠在一起.(7分)
(1)如图1,当OB平分∠COD时,则∠AOD和∠BOC的和是 度?
(2)如图2,当OB不平分∠COD时,则∠AOD和∠BOC的和是 度?
请说明理由
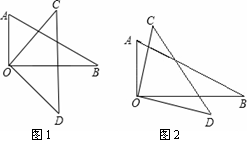 |
查看答案和解析>>
科目:初中数学 来源: 题型:
端午节期间,扬州某商场为了吸引顾客,开展有奖促销活动,设立了一个可以自由转动的转盘,转盘被分成4个面积相等的扇形,四个扇形区域里分别标有“10元”、“20元”、“30元”、“40元”的字样(如图).规定:同一日内,顾客在本商场每消费满100元就可以转动转盘一次,商场根据转盘指针指向区域所标金额返还相应数额的购物券,某顾客当天消费240元,转了两次转盘.
(1)该顾客最少可得 元购物券,最多可得 元购物券;
(2)请用画树状图或列表的方法,求该顾客所获购物券金额不低于50元的概率.
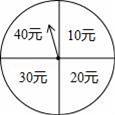

查看答案和解析>>
科目:初中数学 来源: 题型:
兴义市进行城区规划,工程师需测某楼AB的高度,工程师在D得用高2m的测角仪CD,测得楼顶端A的仰角为30°,然后向楼前进30m到达E,又测得楼顶端A的仰角为60°,楼AB的高为( )
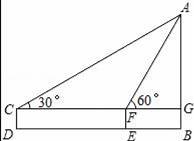

A.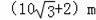
 B.
B.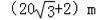
 C.
C.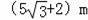
 D.
D.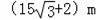

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com