【题目】如图，点A，O，B在同一直线上，射线OD和射线OE分别平分∠AOC和∠BOC．
（1）求∠DOE的度数；
（2）写出图中所有互为余角的角．
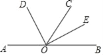
【答案】(1)90°;(2)见解析.
【解析】
(1)根据邻补角定义得∠AOC+∠BOC=180°，由角平分线定义得∠COD=
∠AOC，∠COE=∠BOC，所以∠COD+∠COE=（∠AOC+∠BOC）=90°.即∠DOE=90°.
(2)根据（1）的结论，可以得到互余的角.
解：（1）∵点A，O，B在同一条直线上，
∴∠AOC+∠BOC=180°，
∵射线OD和射线OE分别平分∠AOC和∠BOC，
∴∠COD=∠AOC，∠COE=∠BOC
∴∠COD+∠COE=（∠AOC+∠BOC）=90°，
∴∠DOE=90°；
（2）互为余角的角有：
∠COD和∠COE，∠AOD和∠BOE，∠AOD和∠COE，∠COD和∠BOE．
科目：初中数学 来源： 题型：
【题目】如图，在数轴上有三个点A、B、C，请回答下列问题．
(1)A、B、C三点分别表示什么数？它们到原点的距离分别是多少？
(2)将点B向左移动3个单位长度后，三个点所表示的数中最小的数是多少？
(3)将点A向右移动4个单位长度后，三个点所表示的数中最小的数是多少？
(4)要怎样移动A、B、C三点中的两个点，才能使三个点表示的数相同？移动方法唯一吗？若不是，请任意选择一种回答，
查看答案和解析>>
科目：初中数学 来源： 题型：
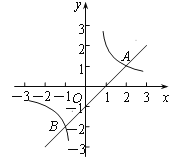
【题目】如图，直线
与双曲线
相交于A（2，1）、B两点．
（1）求m及k的值；
（2）不解关于x、y的方程组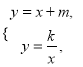
直接写出点B的坐标；
（3）直线
经过点B吗？请说明理由．
【答案】（1）m=－1，k=2；（2）（－1，－2）；（3）经过
【解析】试题分析：（1）把A（2，1）分别代入直线
与双曲线
即可求得结果；
（2）根据函数图象的特征写出两个图象的交点坐标即可；
（3）把x=－1，m=－1代入
即可求得y的值，从而作出判断.
（1）把A（2，1）分别代入直线
与双曲线
的解析式得m=－1，k=2；
（2）由题意得B的坐标（－1，－2）；
（3）当x=－1，m=－1代入
得y=－2×(－1)+4×(－1)=2－4=－2
所以直线
经过点B(－1，－2).
考点：反比例函数的性质
点评：反比例函数的性质是初中数学的重点，是中考常见题，一般难度不大，需熟练掌握.
【题型】解答题
【结束】
20
【题目】某气球内充满了一定质量的气球，当温度不变时，气球内气球的压力p(千帕)是气球的体积V(米2)的反比例函数，其图象如图所示(千帕是一种压强单位)
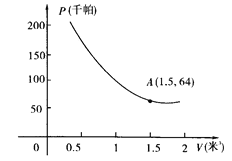
（1）写出这个函数的解析式；
（2）当气球的体积为0.8立方米时，气球内的气压是多少千帕；
（3）当气球内的气压大于144千帕时，气球将爆炸，为了安全起见，气球的体积应不小于多少立方米。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一架梯子的长度为25米，斜靠在墙上，梯子低部离墙底端为7米．
（1）这个梯子顶端离地面有 米；
（2）如果梯子的顶端下滑了4米，那么梯子的底部在水平方向滑动了几米？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在¨ABCD中，过点D作DE⊥AB与点E，点F在边CD上，DF=BE,连接AF,BF
（1）求证：四边形BFDE是矩形；
（2）若CF=3，BF=4，DF=5，求证：AF平分∠DAB.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】先化简，再求值：
(1)2xy－
(4xy－8x2y2)＋2(3xy－5x2y2)，其中x＝
，y＝－3.
(2)－a2b＋(3ab2－a2b)－2(2ab2－a2b)，其中a＝1，b＝－2.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在四边形ABCD中，CA平分∠DCB，∠ADC=∠BAC=90°． 
（1）求证：AC2=BCDC；
（2）若BC=5，DC=1，求线段AD的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
