Question

1．已知A（a，0），B（b，0），C（b，c）满足$\sqrt{a+c}$+（b-3）²=0，且|a-1|≤0
（1）求A、B、C的坐标；
（2）D是y轴上的一个动点．
①若S_△DAB=S_△DBC，求D的坐标．
②若D在y轴负半轴上运动，AF，CF分别平分∠GAB，∠BCE且交于点F．
（3）请探索∠F与∠ADC的数量关系；
（4）若OD=1，求∠F的度数．

Answer 1

分析 （1）根据非负数的性质解得a、b、c的值，可以确定A、B、C的坐标．
（2）根据△DBC的面积=$\frac{3}{2}$，可以求出D点坐标．
（3）根据四边形的性质，利用方程的思想解决问题．
（4）根据∠ADC=45°，再利用（3）的结论可以求出∠F．

解答 解：（1）∵$\sqrt{a+c}$+（b-3）²=0，且|a-1|≤0，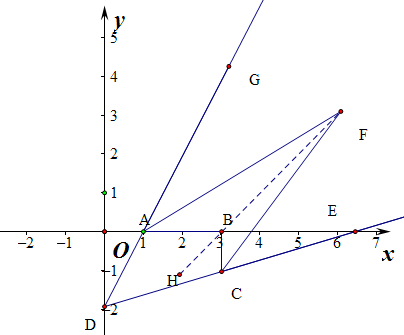
且$\sqrt{a+c}$≥0，（b-3）²≥0，|a-1|≥0，
∴$\sqrt{a+c}$=0，（b-3）²=0，|a-1|=0，
∴a=1，b=3，c=-1，
∴A（1，0），B（3，0），C（3，-1）．
（2）设D（0，m），
∵S_△DAB=S_△DBC，
∴$\frac{1}{2}$×2×|m|=$\frac{1}{2}$×1×3
∴m=±$\frac{3}{2}$，
∴D点坐标（0，$\frac{3}{2}$）或（0，-$\frac{3}{2}$）．
（3）延长FB到H，
由题意可以设∠GAF=∠FAE=x，∠BCF=∠FCE=y，
∵∠ABH=x+∠AFB，∠CBH=y+∠BFC，
∴∠ABH+∠CBH=x+y+∠AFB+∠BFC，∵∠ABC=90°，
∴x+y=90°-∠AFC        ①，
在四边形ADCB中，∠ADC+∠DCB+∠ABC+∠BAD=360°，
∴∠ADC+180°-2x+180°-2y+90°=360°     ②
①代入②得到∠ADC=90°-2∠AFC．
（4）∵OD=1，BC=1，
∴OD=BC，
∵OD∥CB
∴四边形ODCB是平行四边形，
∵∠DOB=90°，
∴四边形ODCB是矩形，
∴∠ODC=90°，
∵OA=OD，
∴∠ODA=45°，
∴∠ADC=45°，
∵∠ADC=90°-2∠AFC，
∴∠AFC=22.5°．

点评 本题考查了非负数的性质、三角形的面积的计算，四边形的性质和判定等知识，利用方程的思想，探讨两个角之间的关系是解第3问题的关键．