
【题目】如图,已知CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于点O,且AO平分∠BAC,那么图中全等三角形共有( )对. 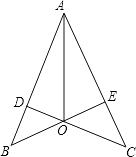
A.2
B.3
C.4
D.5
【答案】C
【解析】解:∵CD⊥AB,BE⊥AC,AO平分∠BAC
∴∠ADO=∠AEO=90°,∠DAO=∠EAO
∵AO=AO
∴△ADO≌△AEO;(AAS)
∴OD=OE,AD=AE
∵∠DOB=∠EOC,∠ODB=∠OEC=90°
∴△BOD≌△COE;(ASA)
∴BD=CE,OB=OC,∠B=∠C
∵AE=AD,∠DAC=∠CAB,∠ADC=∠AEB=90°
∴△ADC≌△AEB;(ASA)
∵AD=AE,BD=CE
∴AB=AC
∵OB=OC,AO=AO
∴△ABO≌△ACO.(SSS)
所以共有四对全等三角形.
故选C.
共有四对.分别为△ADO≌△AEO,△ADC≌△AEB,△ABO≌△ACO,△BOD≌△COE.做题时要从已知条件开始结合图形利用全等的判定方法由易到难逐个寻找.


 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:
【题目】下列直线是圆的切线的是( )
A. 经过半径外端的直线B. 垂直于半径的直线
C. 与圆有公共点的直线D. 圆心到直线的距离等于这个圆的半径长的直线
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=90°, 
(1)CD平分∠ACB,BE⊥CD,垂足E在CD的延长线上,BE的延长线交CA的延长线于M,补全图形,并探究BE和CD的数量关系,并说明理由;
(2)若BC上有一动点P,且∠BPQ= ![]() ∠ACB,BQ⊥PQ于Q,PQ交AB于F,试探究BQ和PF之间的数量关系,并证明你的结论.
∠ACB,BQ⊥PQ于Q,PQ交AB于F,试探究BQ和PF之间的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现在网购越来越多地成为人们的一种消费方式,刚刚过去的2014年的“双11”网上促销活动中,天猫和淘宝的支付交易额突破57000000000元,将57000000000元用科学记数法表示为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把能平分四边形面积的直线称为“好线”.利用下面的作图,可以得到四边形的“好线”:在四边形ABCD(图2)中,取对角线BD的中点O,连接OA、OC.得折线AOC,再过点O作OE∥AC交CD于E,则直线AE即为四边形ABCD的一条“好线”.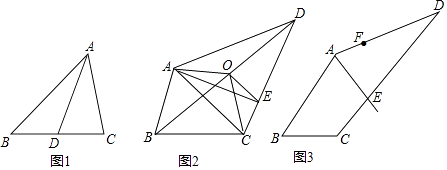
(1)如图(1),试说明中线AD平分△ABC的面积;
(2)如图(2),请你探究四边形ABCO的面积和四边形ABCD面积的关系,并说明理由;
(3)解:在图(2)中,请你说明直线AE是四边形ABCD的一条“好线”;
(4)如图(3),若AE为一条“好线”,F为AD边上的一点,请作出四边形ABCD经过F点的“好线”,并对你的画图作适当说明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com