Question

【题目】如图，矩形ABCD中，BC=2AB，对角线相交于O，过C点作CE⊥BD交BD于E点，H为BC中点，连接AH交BD于G点，交EC的延长线于F点，下列5个结论：①EH=AB；②∠ABG=∠HEC；③△ABG≌△HEC；④S△GAD=S四边形GHCE ， ⑤CF=BD．正确的有（ ）个．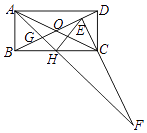
A.1
B.2
C.3
D.4

Answer 1

【答案】C
【解析】解：①在△BCE中，∵CE⊥BD，H为BC中点， ∴BC=2EH，又BC=2AB，
∴EH=AB，①正确；
②由①可知，BH=HE∴∠EBH=∠BEH，
又∠ABG+∠EBH=∠BEH+∠HEC=90°，
∴∠ABG=∠HEC，②正确；
③由AB=BH，∠ABH=90°，得∠BAG=45°，
同理：∠DHC=45°，∴∠EHC＞∠DHC=45°，
∴△ABG≌△HEC，③错误；
④作AM⊥BD，则AM=CE，△AMD≌△CEB，
∵AD∥BC，
∴△ADG∽△HGB，
∴ =2，
即△ABG的面积等于△BGH的面积的2倍，
根据已知不能推出△AMG的面积等于△ABG的面积的一半，
即S△GAD≠S四边形GHCE ，
∴④错误
⑤∠ECH=∠CHF+∠F=45°+∠F，
又∠ECH=∠CDE=∠BAO，∠BAO=∠BAH+∠HAC，
∴∠F=∠HAC，
∴CF=BD，⑤正确．
正确的有3个．
故选C．
根据BC=2AB，H为BC中点，可得△ABH为等腰直角三角形，HE=BH=HC，可得△CEH为等腰三角形，又∠BCD=90°，CE⊥BD，利用互余关系得出角的相等关系，根据基本图形判断全等三角形，特殊三角形进行判断．