
【题目】如图,小明有5张写着不同数的卡片,请你按照题目要求抽出卡片,完成下列问题:
(1)从中取出3张卡片,使这3张卡片上数字的乘积最大,如何抽取?最大值是多少?
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,如何抽取?最小值是多少?

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】同学们都知道:|5|在数轴上表示数5的点与原点的距离,而|5-(-2)|表示5与-2之差的绝对值,实际上也可理解为5与-2两数在数轴上所对应的两点之间的距离.请你借助数轴进行以下探索:
![]()
(1)则![]() 表示 的距离.
表示 的距离.
(2)数轴上表示x与 7的两点之间的距离可以表示为 .
(3)如果|x-2|=5,则x= .
(4)同理|x+1|+|x-2|表示数轴上有理数x所对应的点到-1和2所对应的点的距离之和,请你找出所有符合条件的整数x,使得|x+1|+|x-2|=3,这样的整数是 .
(5)由以上探索猜想对于任何有理数x,|x+3|+|x-6|的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的运算程序中,若开始输入的x值为48,我们发现第一次输出的结果为24,第二次输出的结果为12,…,则第2018次输出的结果为________.
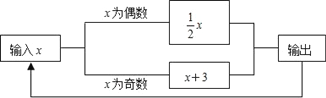
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(![]() +
+![]()
![]() )×(-60) (2) (-
)×(-60) (2) (-![]() )×(-3
)×(-3![]() )÷(-1
)÷(-1![]() )÷3;
)÷3;
(3) (-5)×(-3![]() )+(-7)×(-3
)+(-7)×(-3![]() )+12×(-3
)+12×(-3![]() ) (4) 19
) (4) 19![]() ×(-8)
×(-8)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足 ![]() =
= ![]() ,连接AF并延长交⊙O于点E,连接AD,DE,若CF=2,AF=3,给出下列结论:①△ADF∽△AED;②FG=2;③tanE=
,连接AF并延长交⊙O于点E,连接AD,DE,若CF=2,AF=3,给出下列结论:①△ADF∽△AED;②FG=2;③tanE= ![]() ;④S△DEF=4
;④S△DEF=4 ![]() ,其中正确的是( )
,其中正确的是( ) 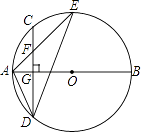
A.①②③
B.②③④
C.①②④
D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )

A. BE=DF B. BF=DE C. AE=CF D. ∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
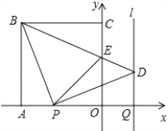
【题目】如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(﹣4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s).
(1)∠PBD的度数为 ,点D的坐标为 (用t表示);
(2)当t为何值时,△PBE为等腰三角形?
(3)探索△POE周长是否随时间t的变化而变化?若变化,说明理由;若不变,试求这个定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次函数y=kx-6中,已知y随x的增大而减小.下列关于反比例函数y=![]()
的描述,其中正确的是( )
A. 当x>0时,y>0 B. y随x的增大而增大
C. y随x的增大而减小 D. 图像在第二、四象限
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com