
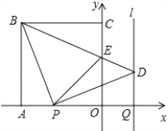
����Ŀ����ͼ��������OABC�ı�OA��OC���������ϣ���B������Ϊ����4��4������P�ӵ�A��������ÿ��1����λ���ȵ��ٶ���x�����O�˶�����Q�ӵ�Oͬʱ����������ͬ���ٶ���x����������˶����涨��P�����Oʱ����QҲֹͣ�˶�������BP����P����BP�Ĵ��ߣ������Qƽ����y���ֱ��l�ཻ�ڵ�D��BD��y�ύ�ڵ�E������PE�����P�˶���ʱ��Ϊt��s����
��1����PBD�Ķ���Ϊ ����D������Ϊ ����t��ʾ����
��2����tΪ��ֵʱ����PBEΪ���������Σ�
��3��̽����POE�ܳ��Ƿ���ʱ��t�ı仯���仯�����仯��˵�����ɣ������䣬���������ֵ��
���𰸡���1��45������t��t������2��tΪ4���![]() ���룻��3����POE�ܳ��Ƕ�ֵ���ö�ֵΪ8��
���룻��3����POE�ܳ��Ƕ�ֵ���ö�ֵΪ8��
�������������������1����֤��BAP�ա�PQD���Ӷ��õ�DQ=AP=t���Ӷ����������PBD�Ķ����͵�D�����꣮
��2��������EBP=45������ͼ1����������Ϊ������һ������ͼ�Σ����õ�EP=AP+CE��������PBE�ױ߲������ʷ�����������ۣ�������������ȫ�ȼ����ɶ���������⣬Ȼ������������ȡ�ᣬ����ȷ������Ҫ���tֵ��
��3���ɣ�2����֤�Ľ���EP=AP+CE�����õ���POE�ܳ�����AO+CO=8���Ӷ�������⣮
�����������1����ͼ1������ɵã�AP=OQ=1��t=t���룩
��AO=PQ��
���ı���OABC�������Σ���AO=AB=BC=OC����BAO=��AOC=��OCB=��ABC=90����
��DP��BP�����BPD=90�������BPA=90�㩁��DPQ=��PDQ��
��AO=PQ��AO=AB����AB=PQ��
����BAP����PQD�У��ߡ�BAP=��PQD����BPA=��PDQ��AB=PQ�����BAP�ա�PQD��AAS������AP=QD��BP=PD���ߡ�BPD=90����BP=PD�����PBD=��PDB=45������AP=t����DQ=t������D����Ϊ��t��t����
�ʴ�Ϊ��45������t��t����
��2������PB=PE������PAB�ա�DQP��PB=PD����ȻPB��PE�����������Ӧ��ȥ��
����EB=EP������PBE=��BPE=45�������BEP=90�������PEO=90�㩁��BEC=��EBC��
����POE����ECB�У��ߡ�PEO=��EBC����POE=��ECB��EP=BE�����POE�ա�ECB��AAS������OE=CB=OC������E���C�غϣ�EC=0��������P���O�غϣ�PO=0����
����B����4��4������AO=CO=4����ʱt=AP=AO=4��
����BP=BE����Rt��BAP��Rt��BCE����BA=BC��BP=BE����Rt��BAP��Rt��BCE��HL������AP=CE��
��AP=t����CE=t����PO=EO=4��t��
�ߡ�POE=90������PE=![]() =
=![]() ��
��
�ӳ�OA����F��ʹ��AF=CE������BF����ͼ2��ʾ������FAB����ECB�У���AB=CB����BAF=��BCE=90����AF=CE�����FAB�ա�ECB����FB=EB����FBA=��EBC��
�ߡ�EBP=45������ABC=90�������ABP+��EBC=45�������FBP=��FBA+��ABP
=��EBC+��ABP=45�������FBP=��EBP��
����FBP����EBP��
���FBP�ա�EBP��SAS������FP=EP����EP=FP=FA+AP=CE+AP����EP=t+t=2t����![]() =2t����ã�t=
=2t����ã�t=![]() ������tΪ4���
������tΪ4���![]() ����ʱ����PBEΪ���������Σ�
����ʱ����PBEΪ���������Σ�
��3����EP=CE+AP����OP+PE+OE=OP+AP+CE+OE=AO+CO=4+4=8�����POE�ܳ��Ƕ�ֵ���ö�ֵΪ8��




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������OABC�Ķ���A��C�ֱ���x���y���ϣ���B������Ϊ��4��6����˫����y= ![]() ��x��0����ͼ��BC���е�D������AB���ڵ�E������DE��
��x��0����ͼ��BC���е�D������AB���ڵ�E������DE��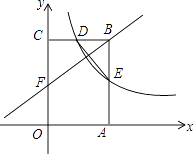
��1����k��ֵ����E�����ꣻ
��2������F�DZ���һ�㣬�ҡ�BCF�ס�EBD����ֱ��FB�Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С����5��д�Ų�ͬ���Ŀ�Ƭ�����㰴����ĿҪ������Ƭ�������������:
��1������ȡ��3�ſ�Ƭ��ʹ��3�ſ�Ƭ�����ֵij˻������γ�ȡ�����ֵ�Ƕ��٣�
��2������ȡ��2�ſ�Ƭ��ʹ��2�ſ�Ƭ���������������С����γ�ȡ����Сֵ�Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
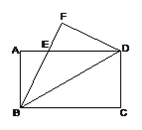
����Ŀ����ͼ�ѳ������ضԽ����۵����غϲ���Ϊ��EBD��
(1) ��EBD�ǵ�����������Ϊʲô��
��2�� ��AB��12cm��BC��18cm����AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ǽ�����ABCD�Ե�OΪ���İ�˳ʱ�뷽��ֱ���ת90����180����270�����γɵ�ͼ�Ρ���![]() ��AB=2����ͼ����Ӱ���ֵ����Ϊ�� ��
��AB=2����ͼ����Ӱ���ֵ����Ϊ�� ��
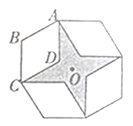
A. 12��4![]() B. 5 C. 12-4
B. 5 C. 12-4![]() D. 6
D. 6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC��һ��������������ϣ���BC=120mm����AD=80mm��Ҫ�����ӹ��ɳ��������PQMN��ʹ������PQMN�ı�QM��BC�ϣ�������������P��N�ֱ���AB��AC�ϣ���������������PQMN���S�����ֵ�� 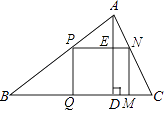
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������������У� 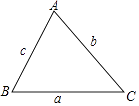
��1������ ![]() ��
�� ![]() ��
�� ![]() ֮��Ĺ�ϵ����֤����
֮��Ĺ�ϵ����֤����
��2������cosC��a��b��c֮��Ĺ�ϵ����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt�SABC�У���C = 90����б��ABΪ��������������ABDE���������ζԽ��߽��ڵ�O������OC����֪AC=6��OC=![]() ����ֱ�DZ�BC�ij�Ϊ___________
����ֱ�DZ�BC�ij�Ϊ___________

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ʾ��AOB��ֽƬ��OCƽ�֡�AOB����ͼ2�ѡ�AOB��OC���۳ɡ�COB��OA��OB�غϣ�����O����һ������OE��ʹ��BOE=![]() ��EOC������OE�ѽǼ�������������õ���3����������һ����Ϊ76�������AOB=_____________�㣮
��EOC������OE�ѽǼ�������������õ���3����������һ����Ϊ76�������AOB=_____________�㣮

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com