
【题目】如图,Rt⊿ABC中,∠C = 90,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=6,OC=![]() ,则直角边BC的长为___________
,则直角边BC的长为___________

【答案】8
【解析】分析:过O作OF⊥BC,过A作AM⊥OF,只要证明△AOM和△BOF全等推出AM=OF,OM=FB,根据题意得出四边形ACFM为矩形,从而得出AM=CF=6,OF=CF,得出△OCF为等腰直角三角形,根据OC=![]() 得出 CF=OF=7,根据FB=OM=OF-FM求出FB的值,最后根据BC=CF+BF得出答案.
得出 CF=OF=7,根据FB=OM=OF-FM求出FB的值,最后根据BC=CF+BF得出答案.
详解:过O作OF⊥BC,过A作AM⊥OF, ∵四边形ABDE为正方形,
∴∠AOB=90°,OA=OB, ∴∠AOM+∠BOF=90°,
又∠AMO=90°,∴∠AOM+∠OAM=90°, ∴∠BOF=∠OAM,
在△AOM和△BOF中, ∠AMO=∠OFB=90°∠OAM=∠BOF,OA=OB,
∴△AOM≌△BOF(AAS), ∴AM=OF,OM=FB, 又∠ACB=∠AMF=∠CFM=90°,
∴四边形ACFM为矩形, ∴AM=CF,AC=MF=6, ∴OF=CF,
∴△OCF为等腰直角三角形, ∵OC=![]() , ∴根据勾股定理得:CF2+OF2=OC2,
, ∴根据勾股定理得:CF2+OF2=OC2,
解得:CF=OF=7, ∴FB=OM=OF-FM=7-6=1, 则BC=CF+BF=7+1=8.



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
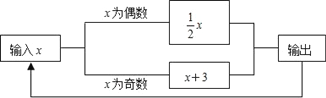
【题目】如图所示的运算程序中,若开始输入的x值为48,我们发现第一次输出的结果为24,第二次输出的结果为12,…,则第2018次输出的结果为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
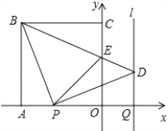
【题目】如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(﹣4,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与y轴交于点E,连接PE.设点P运动的时间为t(s).
(1)∠PBD的度数为 ,点D的坐标为 (用t表示);
(2)当t为何值时,△PBE为等腰三角形?
(3)探索△POE周长是否随时间t的变化而变化?若变化,说明理由;若不变,试求这个定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在开展“好书伴我成长”的读书活动中,某中学为了解八年级300名学生读书情况,随机调查了八年级50名学生读书的册数.统计数据如下表所示:

(1)求这50个样本数据的平均救,众数和中位数.
(2)根据样本数据,估计该校八年级300名学生在本次活动中读书多于2册的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠A,∠B,∠C的对边分别记为![]() ,
,![]() ,
,![]() ,由下列条件不能判定△ABC为直角三角形的是( ).
,由下列条件不能判定△ABC为直角三角形的是( ).
A.∠A+∠B=∠C
B.∠A∶∠B∶∠C =1∶2∶3
C.![]()
D.![]() ∶
∶![]() ∶
∶![]() =3∶4∶6
=3∶4∶6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次函数y=kx-6中,已知y随x的增大而减小.下列关于反比例函数y=![]()
的描述,其中正确的是( )
A. 当x>0时,y>0 B. y随x的增大而增大
C. y随x的增大而减小 D. 图像在第二、四象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两组卡片共5张,A中三张分别写有数字2,4,6,B中两张分别写有3,5.它们除了数字外没有任何区别.
(1)随机地从A中抽取一张,求抽到数字为2的概率;
(2)随机地分别从A、B中各抽取一张,请你用画树状图或列表的方法表示所有等可能的结果,现制定这样一个游戏规则:若选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?
(3)如果不公平请你修改游戏规则使游戏规则对甲乙双方公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:问题:如图1,在菱形ABCD和菱形BEFG中,∠ABC=∠BEF=60°,点A,B,E在同一条直线上,P是线段DF的中点,连接PG,PC,探究PG与PC的位置关系。
(1)请你写出上面问题中线段PG与PC的位置关系,并说明理由;
(2)将图1中的菱形BEFG绕点B顺时针旋转,使菱形BEFG的对角线BF恰好与菱形ABCD的边AB在同一条直线上,原问题中的其他条件不变(如图2).你在(1)中得到的结论是否发生变化?写出你的猜想并加以证明,
(3)将菱形ABCD和菱形BEFG均改成正方形,如图3,P为DF的中点,此时PG与PC的位置关系和数量关系分别是什么?直接写出答案。



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com