
分析 将算式变形为$\frac{201{7}^{2}}{(2017-1)^{2}+(2017+1)^{2}-2}$,根据完全平方公式得到原式=$\frac{201{7}^{2}}{201{7}^{2}-2017×2+1+201{7}^{2}+2017×2+1-2}$,再化简后约分即可求解.
解答 解:$\frac{201{7}^{2}}{201{6}^{2}+201{8}^{2}-2}$
=$\frac{201{7}^{2}}{(2017-1)^{2}+(2017+1)^{2}-2}$
=$\frac{201{7}^{2}}{201{7}^{2}-2017×2+1+201{7}^{2}+2017×2+1-2}$
=$\frac{201{7}^{2}}{2×201{7}^{2}}$
=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 考查了完全平方公式,解题的关键是将算式变形为$\frac{201{7}^{2}}{(2017-1)^{2}+(2017+1)^{2}-2}$.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
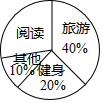 某企业为了解职工业余爱好,组织对本企业150名职工业余爱好进行调查,制成了如图所示的扇形统计图,则在被调查的职工中,爱好旅游和阅读的人数分别是( )
某企业为了解职工业余爱好,组织对本企业150名职工业余爱好进行调查,制成了如图所示的扇形统计图,则在被调查的职工中,爱好旅游和阅读的人数分别是( )| A. | 45,30 | B. | 60,40 | C. | 60,45 | D. | 40,45 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,FG为⊙O的直径,$\widehat{HF}$=$\widehat{HG}$,E为$\widehat{HF}$上一点,延长FE至点A,使EA=EG,连接HG.
如图,FG为⊙O的直径,$\widehat{HF}$=$\widehat{HG}$,E为$\widehat{HF}$上一点,延长FE至点A,使EA=EG,连接HG.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,用若干个全等的正五边形可以拼成一个环状,图中所示的是前3个正五边形的拼接情况,要完全拼成一个圆环共需要的正五边形个数是( )
如图,用若干个全等的正五边形可以拼成一个环状,图中所示的是前3个正五边形的拼接情况,要完全拼成一个圆环共需要的正五边形个数是( )| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AD∥BC,AD⊥AB,点A,B在y轴上,CD与x轴交于点E(2,0),且AD=DE,BC=2CE,则BD与x轴交点F的横坐标为( )
如图,AD∥BC,AD⊥AB,点A,B在y轴上,CD与x轴交于点E(2,0),且AD=DE,BC=2CE,则BD与x轴交点F的横坐标为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9分米 | B. | 15分米 | C. | 5分米 | D. | 8分米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com