
【题目】(1)如图 1 所示,△ ABC 和△ AEF 为等边三角形,点 E 在△ ABC 内部,且 E 到点 A、B、C 的距离分别为 3、4、5,求∠AEB 的度数.
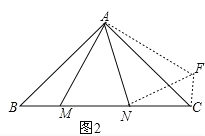
(2)如图 2,在△ ABC 中,∠CAB=90°,AB=AC,M、N 为 BC 上的两点,且∠MAN=45°,MN2 与 NC2+BM2 有何关系?说明理由.

【答案】(1)150°;(2)MN2=NC2+BM2.
【解析】
(1)根据等边三角形的性质和全等三角形的判定可知CF=BE=4,∠AEB=∠AFC,再由勾股定理的逆定理可知∠CFE=90°,从而可求出∠AEB;
(2)根据旋转的性质和全等三角形的判定可知CF=BM 、MN=FN,由题意可证∠FCN=90°,进而可证明MN2=NC2+BM2.
解:(1)连接 FC,如图1所示:
∵△ABC 和△ AEF 为等边三角形,
∴AE=AF=EF=3,AB=AC,∠AFE=60°,∠BAC=∠EAF=60°,
∴∠BAE=∠CAF=60°﹣∠CAE,
在△ BAE 和△ CAF 中,
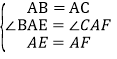
∴△BAE≌△CAF(SAS),
∴CF=BE=4,∠AEB=∠AFC,
又∵EF=3,CE=5,
∴CE2=EF2+CF2,
∴∠CFE=90°,
∵∠AFE=60°,
∴∠AFC=90°+60°=150°,
∴∠AEB=∠AFC=150°;
(2)MN2=NC2+BM2,理由如下:
将△ ABM 绕 A 点逆时针旋转 90°,得到△ AFC,如图 2 所示: 则 AM=AF,CF=BM,∠BAM=∠CAF,∠B=∠ACF,
∵∠BAC=90°,∠MAN=45°,
∴∠NAF=∠CAN+∠FAC=∠CAN+∠BAM=90°﹣45°=45°=∠MAN,
在△ MAN 和△ FAN 中,

∴△MAN≌△FAN(SAS),
∴MN=FN,
∵∠BAC=90°,AB=AC,
∴∠B=∠ACB=45°,
∵∠B=∠ACF,
∴∠ACF=45°,
∴∠FCN=90°,
由勾股定理得:NF2=CF2+CN2,
∵CF=BM,NF=MN,
∴MN2=NC2+BM2.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】(阅读材料)
平面直角坐标系中,点P(x,y)的横坐标x的绝对值表示为|x|,纵坐标y的绝对值表示为|y|,我们把点P(x,y)的横坐标与纵坐标的绝对值之和叫做点P(x,y)的勾股值,记为[P],即[P]=|x|+|y|(其中的“+“是四则运算中的加法),例如点P(1,2)的勾股值[P]=|1|+|2|=3.
(解决问题)
(1)求点A(-2.4),B(![]() +
+![]() -
-![]() )的勾股值[A],[B];
)的勾股值[A],[B];
(2)若点M在x轴的上方,其横,纵坐标均为整数,且[M]=3,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=ax2+bx+c(a<0)的图象如图所示,且关于x的方程ax2+bx+c=k有两个不相等的实根,则常数k的取值范围是( )
A.0<k<4
B.﹣3<k<1
C.k<﹣3或k>1
D.k<4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中考体育测试前,某区教育局为了了解选报引体向上的初三男生的成绩情况,随机抽测了本区部分选报引体向上项目的初三男生的成绩,并将测试得到的成绩绘成了下面两幅不完整的统计图:
请你根据图中的信息,解答下列问题:
(1)写出扇形图中a=%,并补全条形图;
(2)在这次抽测中,测试成绩的众数和中位数分别是 个、个.
(3)该区体育中考选报引体向上的男生共有1800人,如果体育中考引体向上达6个以上(含6个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中,∠A=90°,AB=AC,点D为BC的中点.
(1)如图①,若点E、F分别为AB、AC上的点,且DE⊥DF,求证:BE=AF;
(2)若点E、F分别为AB、CA延长线上的点,且DE⊥DF,那么BE=AF吗?请利用图②说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场柜台销售每台进价分别为160元、120元的![]() 、
、![]() 两种型号的电器,下表是近两周的销售情况:
两种型号的电器,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
|
| ||
第一周 | 3台 | 4台 | 1200元 |
第二周 | 5台 | 6台 | 1900元 |
(进价、售价均保持不变,利润=销售收入—进货成本)
(1)求![]() 、
、![]() 两种型号的电器的销售单价;
两种型号的电器的销售单价;
(2)若商场准备用不多于7500元的金额再采购这两种型号的电器共50台,求![]() 种型号的电器最多能采购多少台?
种型号的电器最多能采购多少台?
(3)在(2)中商场用不多于7500元采购这两种型号的电器共50台的条件下,商场销售完这50台电器能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com