
����Ŀ�����������죩
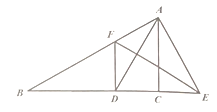
����1����ͼ1�����ı���ABCD�У�CB=CD����B=��ADC=90�㣬��BCD=120�㣮E��F�ֱ���AB��AD�ϵĵ㣮�ҡ�ECF=60�㣮̽��ͼ���߶�BE��EF��FD֮���������ϵ��С��ͬѧ̽��������ķ����ǣ��ӳ�FD����G��ʹDG=BE������CG����֤����CBE�ա�CDG����֤����CEF�ա�CGF�����ó�����ȷ������ ��
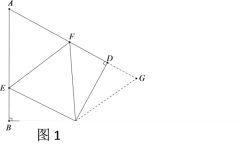
��̽��˼����
����2����ͼ2����������1��������Ϊ���ı���ABCD�У�CB=CD����ABC+��ADC=180�㣬��ECF=![]() ��BCD������1�Ľ����Ƿ���Ȼ��������˵�����ɣ�
��BCD������1�Ľ����Ƿ���Ȼ��������˵�����ɣ�
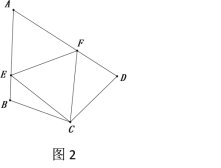
����չ���죩
����3����ͼ3��������2�������£�����E��AB���ӳ����ϣ���F��DA���ӳ����ϣ���BE=2��DF=8����EF�ij�����ֱ��д���𰸣�
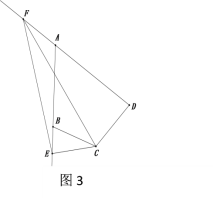
���𰸡���1��EF=BE+DF����2������1�н�����Ȼ����,���ɼ���������3��6.
��������
�ɡ�CEF�ա�CGF��֪CE=CG���ɡ�ECF=60�㣬��BCD=120���֤��FCG=60�㣬�Ӷ���֪��ECF�ա�FCG���ó�EF=GF���Ӷ��ó�EF=BE+DF��ͬ���ɵó���2����3����
��1��EF=BE+DF�����ɣ�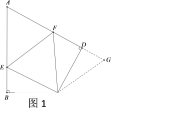
�ӳ�FD����G,ʹDG=BE,����CG��
�ڡ�CBE���CDG��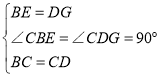
���CBE�ա�CDG��SAS����
��CE=CG����BCE=��DCG��
�ߡ�BCD=120�㣬
���ECG=120��
�ߡ�ECF=60�㣬
���ECF=��GCF��
�ڡ�CEF�͡�CGF��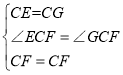 ,
,
���CEF�ա�CGF��
��EF=GF��
��EF=DF+DG=DF+BE
��2���⣺����1�н�����Ȼ����,��ͼ,
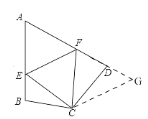
���ɣ��ӳ�FD����G.ʹDG=BE.����CG��
�ߡ�ABC+��ADC=180�㣬��CDG+��ADC=180�㣬
���ABC=��GDC,�ڡ�CBE�͡�CDG��,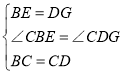
���CBE�ա�CDG(SAS)��
��CE=CG����BCE=��DCG��
���BCD=��ECG��
�ߡ�ECF=![]() ��BCD
��BCD
���ECF=![]() ��ECG
��ECG
���ECF=��GCF��
�ڡ�CEF�͡�CGF��,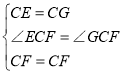
���CEF�ա�CGF��
��EF=GF��
��EF=DF+DG=DF+BE
��3��EF=6����Ϊ��ʱDF=EF+BE�����ɣ���ͼ3��
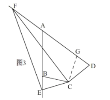
�ӳ�FD����G��ʹDG=BE������CG��
�ߡ�ABC+��ADC=180�㣬��CDG+��ADC=180�㣬
���ABC=��GDC���ڡ�CBE�͡�CDG��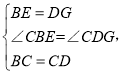 ���CBE�ա�CDG(SAS)��
���CBE�ա�CDG(SAS)��
��CE=CG����BCE=��DCG��
���BCD=��ECG��
�ߡ�ECF=![]() ��BCD
��BCD
���ECF=![]() ��ECG
��ECG
���ECF=��GCF��
�ڡ�CEF�͡�CGF��,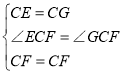
���CEF�ա�CGF��
��EF=GF��
��EF=DF+DG=DF+BE



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ���������˶������ָ���A��B��A��B��C��5������A���DZ߳�Ϊa m�������Σ�C���DZ߳�Ϊc m�������Σ�
(1)��ʽ��ʾÿ��B�������γ��ص��ܳ�������ʽ�ӻ���
(2)��ʽ��ʾ�����������˶������ܳ�������ʽ�ӻ���
(3)���a��40��c��10���������������˶����������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����![]() �У�
��![]() ��
��![]() ƽ���ߣ�
ƽ���ߣ�![]() �Ĵ�ֱƽ���߷ֱ�
�Ĵ�ֱƽ���߷ֱ�![]() �ӳ����ڵ�
�ӳ����ڵ�![]() .��֤��
.��֤��![]() .
.
֤������![]() ƽ��
ƽ��![]()
��![]()
![]() (��ƽ���ߵĶ���)
(��ƽ���ߵĶ���)
��![]() ��ֱƽ��
��ֱƽ��![]()
�� ![]() ���߶δ�ֱƽ�����ϵĵ㵽�߶������˵������ȣ�
���߶δ�ֱƽ�����ϵĵ㵽�߶������˵������ȣ�
��![]() �� ��
�� ��
��![]() ������������
������������
��![]() �� ��
�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�鳤5��4�ĵ�̺��Ϊ��������������ᡢ���ݵ���ɫ���ƣ�ͼ����Ӱ���֣�����֪��ɫ���ƵĿ�����ͬ����ռ�����������̺�����![]() ��
��
��1������ɫ���ƵĿ��ȣ�
��2�������̺��ɫ���Ʋ���ÿƽ�������200Ԫ�����ಿ��ÿƽ�������100Ԫ�����̺������ۣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AD��BC��E��AB���е㣬����DE���ӳ���CB���ӳ����ڵ�F����G�ڱ�BC�ϣ��ҡ�GDF����ADF��
��1����֤����ADE�ա�BFE��
��2������EG���ж�EG��DF��λ�ù�ϵ��˵�����ɣ�
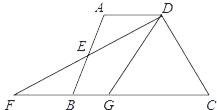
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������и��⣺
��1������1��2018+3��2��������3.14��0
��2����x+3��2��x2
��3����x+2����3x��y����3x��x+y��
��4����2x+y+1����2x+y��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Ϊ60cm����Ϊx(cm)�Ĵ��α��ָ�Ϊ7С�飬����Ӱ A�� B�⣬����5������״����С��ȫ��ͬ��С�����Σ���϶�һ�߳�Ϊ y (cm)��

(1)��գ���ͼ��֪��ÿ��С�����νϳ���һ�߳���_________cm (�ú�y�Ĵ���ʽ��ʾ)��
(2)�ֱ������Ӱ A��B���������������Ӱ A��B���������ú�x��y��ʽ�ӱ�ʾ��
(3)��y=10ʱ����Ӱ A����Ӱ B������������x�ı仯���仯�����������жϣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�У�AB��AC��10cm��BC��8cm����DΪAB���е㣮�����P���߶�BC����3cm/s���ٶ��ɵ�B��C���˶���ͬʱ����Q���߶�CA���ɵ�C��A���˶���
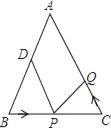
��1������Q���˶��ٶ����P���˶��ٶ���ȣ�����1���BPD���CQP�Ƿ�ȫ�ȣ���˵�����ɣ�
��2������Q���˶��ٶ����P���˶��ٶȲ���ȣ�����Q���˶��ٶ�Ϊ����ʱ���ܹ�ʹ��BPD���CQPȫ�ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������У��ٵ��������εױߵ��е㵽�����ľ�����ȣ��ڵ��������εĸߡ����ߡ���ƽ�������غϣ�����![]() ��
��![]() ����Գƣ���
����Գƣ���![]() һ����
һ����![]() ȫ��;����һ������60�ȵ��������ǵȱ������Σ��ݵ��������εĶԳ����Ƕ��ǵ�ƽ���ߣ���ȷ����ĸ�����( )
ȫ��;����һ������60�ȵ��������ǵȱ������Σ��ݵ��������εĶԳ����Ƕ��ǵ�ƽ���ߣ���ȷ����ĸ�����( )
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com