
����Ŀ����ͼ����֪��ABC�У�AB��AC��10cm��BC��8cm����DΪAB���е㣮�����P���߶�BC����3cm/s���ٶ��ɵ�B��C���˶���ͬʱ����Q���߶�CA���ɵ�C��A���˶���
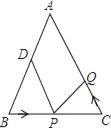
��1������Q���˶��ٶ����P���˶��ٶ���ȣ�����1���BPD���CQP�Ƿ�ȫ�ȣ���˵�����ɣ�
��2������Q���˶��ٶ����P���˶��ٶȲ���ȣ�����Q���˶��ٶ�Ϊ����ʱ���ܹ�ʹ��BPD���CQPȫ�ȣ�
���𰸡���1�������������2����Q���˶��ٶ����P���˶��ٶȲ���ȣ�����Q���˶��ٶ�Ϊ![]() cm/sʱ���ܹ�ʹ��BPD���CQPȫ�ȣ�
cm/sʱ���ܹ�ʹ��BPD���CQPȫ�ȣ�
��������
��1������1���PB=3cm��PC=5cm��CQ=3cm������֪�ɵ�BD=PC��BP=CQ����ABC=��ACB������SAS��֤����BPD�ա�CQP��
��2�������Q���˶��ٶ�Ϊx��x��3��cm/s������ts ��BPD����CQPȫ�ȣ����֪PB=3t cm��PC=��8-3t��cm��CQ=xt cm���ݣ�1��ͬ���ɵõ�BD=PC��BP=CQ��BD=CQ��BP=PCʱ��������ȫ�ȣ���x�Ľ⼴�ɣ�
�⣺��1������1���PB��3cm��PC��5cm�� CQ��3cm��
�ߡ�ABC�У�AB��AC��
������BPD����CQP��
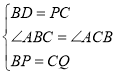 ��
��
���BPD�ա�CQP��SAS����
��2�����Q���˶��ٶ�Ϊx��x��3��cm/s������ts��BPD����CQPȫ�ȣ����֪PB��3t cm��PC����8-3t��cm��CQ��xt cm��
��AB��AC��
���B����C��
����ȫ�������ε��ж�����SAS��֪�������������
�ٵ�BD��PC��BP��CQʱ���ڵ�BD��CQ��BP��PCʱ����������ȫ�ȣ�
�ٵ�BD��PC��BP��CQʱ��
8��3t��5��3t��xt�����x��3��
��x��3��
����ȥ�������
��BD��CQ��BP��PCʱ��
5��xt��3t��8��3t��
��ã�x��![]() ��
��
������Q���˶��ٶ����P���˶��ٶȲ���ȣ�����Q���˶��ٶ�Ϊ![]() cm/sʱ���ܹ�ʹ��BPD����CQPȫ�ȣ�
cm/sʱ���ܹ�ʹ��BPD����CQPȫ�ȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC���Ź�AB�е�D��ֱ���۵���ʹ��A����BC���ϵ�A1����Ϊ��1�β������ۺ�DE��BC�ľ����Ϊh1����ԭֽƬ���ٽ���ADE���Ź�AD�е�D1��ֱ���۵���ʹ��A����DE���ϵ�A2������Ϊ��2�β������ۺ�D1E1��BC�ľ����Ϊh2���������������ϲ�����ȥ����������2019�β�����õ����ۺ�D2018E2018����BC�ľ����Ϊh2019����h1��1����h2019��ֵΪ��____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������죩
����1����ͼ1�����ı���ABCD�У�CB=CD����B=��ADC=90�㣬��BCD=120�㣮E��F�ֱ���AB��AD�ϵĵ㣮�ҡ�ECF=60�㣮̽��ͼ���߶�BE��EF��FD֮���������ϵ��С��ͬѧ̽��������ķ����ǣ��ӳ�FD����G��ʹDG=BE������CG����֤����CBE�ա�CDG����֤����CEF�ա�CGF�����ó�����ȷ������ ��
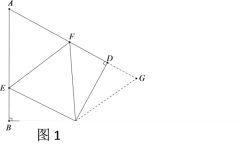
��̽��˼����
����2����ͼ2����������1��������Ϊ���ı���ABCD�У�CB=CD����ABC+��ADC=180�㣬��ECF=![]() ��BCD������1�Ľ����Ƿ���Ȼ��������˵�����ɣ�
��BCD������1�Ľ����Ƿ���Ȼ��������˵�����ɣ�
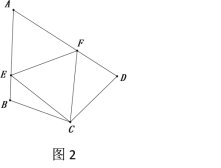
����չ���죩
����3����ͼ3��������2�������£�����E��AB���ӳ����ϣ���F��DA���ӳ����ϣ���BE=2��DF=8����EF�ij�����ֱ��д���𰸣�
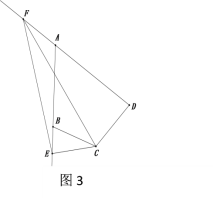
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��A1B1��A2B2��ˮ�������ڵ�����������������������ƽ�е��߶Σ�������һ����Ӿ�˶�����������һ����Ӿ�����ߣ���������A1B1�ϴ�A1������������B1����ͬ�����ٶȷ���A1����Ȼ���ظ��������̣���������A2B2����2m/s���ٶȴ�B2������������A2������ͬ���ٶȻص�B2����Ȼ���ظ��������̣�������ÿ���۷�ʱ�ļ��ٺ�ת��ʱ�䣩�����ס�������ͬʱ���������뿪�ر�B1B2�ľ���Ϊy��m�����˶�ʱ��Ϊt��s�������ζ�ʱ��y��m����t��s���ĺ���ͼ����ͼ2��ʾ��
��1�������ij����� m�����ٶ��� m/s��
��2������������ʱ���ס������˵ڶ���������
��3�����Ӽס�������ͬʱ��ʼ������2����Ϊֹ���ס��ҹ������� �Σ�2����ʱ���Ҿ�ر�B1B2�ľ���Ϊ�����ס�
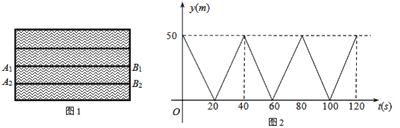
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���֪��A=60�㣬��ABC��ƽ����BD���ACB��ƽ����CE�ཻ�ڵ�O����BOC��ƽ���߽�BC��F�������н��ۣ��١�BOE=60�㣬�ڡ�ABD=��ACE����OE=OD����BC=BE+CD��������ȷ����_________������������ȷ���۵���Ŷ�ѡ�ϣ�
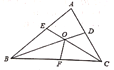
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������и���ABC���DEF��
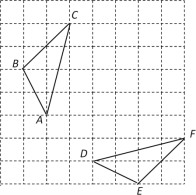
��1����ABC���DEF�Ƿ�ȫ�ȣ�����˵���ɣ���
��2����ABC���DEF�Ƿ����Գƣ�����˵���ɣ���
��3������ABC���DEF����Գƣ��뻭�����ĶԳ���l������ֱ��l�ϻ�����P��ʹPA+PC��С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�E��AB���е㣬AD//EC����AED=��B��
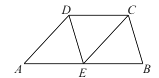
��1����֤����AED�ա�EBC��
��2����AB=6ʱ����CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪BC����ABD�Ľ�ƽ���ߣ�BC=DC����A=��E=30�㣬��D=50�㣮
��1��д��AB=DE�����ɣ�
��2������BCE�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����OABC�ı�OA��x���ϣ���B������Ϊ(8��4)��P�ǶԽ���OB�ϵ�һ�����㣬��D(0��1)��y���ϣ���PC��PD���ʱ����P������Ϊ________��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com