
分析 (1)直接利用根与系数的关系得出关于m的不等式进而求出即可;
(2)利用根与系数的关系以及根的判别式得出关于m的不等式进而求出即可;
(3)把x=0代入方程求解即可.
解答 解:(1)当方程2x2-4mx+3(m2-1)=0方程有两个正根,
∴$\left\{\begin{array}{l}{-\frac{-4m}{2}>0}\\{\frac{3({m}^{2}-1)}{2}>0}\end{array}\right.$,
解得:m>1,
∴当m>1时,方程2x2-4mx+3(m2-1)=0方程有两个正根;
(2)当方程2x2-4mx+3(m2-1)=0方程有两根异号,
∴$\left\{\begin{array}{l}{(-4m)^{2}-4×2×3({m}^{2}-1)>0}\\{\frac{3({m}^{2}-1)}{2}<0}\end{array}\right.$,
解得:-1<m<1,
∴当-1<m<1时,方程2x2-4mx+3(m2-1)=0方程有两根异号;
(3)当方程2x2-4mx+3(m2-1)=0方程有一个根为0,
∴把x=0代入2x2-4mx+3(m2-1)=0得3(m2-1)=0,
解得:m=±1,
∴当m=±1,方程2x2-4mx+3(m2-1)=0方程有一个根为0.
点评 本题考查的知识点是一元二次方程根与系数的关系以及根的判别式等知识,其中由韦达定理(一元二次方程根与系数的关系)结合已知,构造出关于m的不等式组是解答本题的关键.


科目:初中数学 来源: 题型:填空题
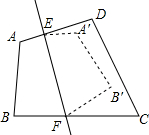 如图,四边形ABCD沿直线EF对着,点A、B的对应点A′,B′落在四边形内部,若∠C+∠D=160°,则∠DEA′+∠CFB′的度数是40°.
如图,四边形ABCD沿直线EF对着,点A、B的对应点A′,B′落在四边形内部,若∠C+∠D=160°,则∠DEA′+∠CFB′的度数是40°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
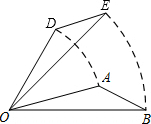 如图,将△AOB绕点O逆时针旋转45°后得到△DOE,若AOB=15°,则∠AOE的度数是( )
如图,将△AOB绕点O逆时针旋转45°后得到△DOE,若AOB=15°,则∠AOE的度数是( )| A. | 25° | B. | 30° | C. | 35° | D. | 40° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com