
【题目】(1)如图①,在△ABC中,∠BAC=90,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D.E证明:DE=BD+CE.
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D. A.E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC,请问结论DE=BD+CE是否成立,若成立,请你给证明:若不存在,请说明理由。
(3)应用:如图③,在△ABC中,∠BAC是钝角,AB=AC,∠BAD>∠CAE,D. A.E三点都在直线m上,且∠BDA=∠AEC=∠BAC,只出现m与BC的延长线交于点F,若BD=5,DE=7,EF=2CE,求△ABD与△ABF的面积之比。

【答案】(1)见解析;(2)成立,理由见解析;(3)2:9
【解析】
(1)证明△ABD≌△CAE,根据全等三角形的性质证明即可;
(2)根据三角形内角和定理证明∠CAE=∠ABD,证明△ABD≌△CAE,根据全等三角形的性质证明即可;
(3)根据(2)的结论求出AE、AD、EF,根据三角形的面积公式计算即可.
(1)证明:∵∠BAC=90°
∴∠BAD+∠CAE=90°
∵CE⊥直线m
∴∠ACE+∠CAE=90°
∴∠BAD=∠ACE
在△ABD和△CAE中
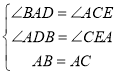
∴△ABD≌△CAE(AAS)
∴BD=AE,AD=CE
∴DE=AE+AD=BD+CE
(2)结论DE=BD+CE成立
证明:∠CAE=180°﹣∠BAC﹣∠BAD,
∠ABD=180°﹣∠ADB﹣∠BAD,
∴∠CAE=∠ABD
在△ABD和△CAE中
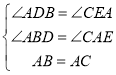
∴△ABD≌△CAE(AAS)
∴BD=AE,AD=CE
∴DE= AE+ AD =BD+CE
(3)由(2)得,△ABD≌△CAE
∴AE=BD=5,
∴AD=DE﹣AE=2
∴EF=2CE=4
∴△ABD与△ABF的面积之比=AD:AF=2:9


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】尺规作图:作点A关于直线l的对称点A'.
已知:直线l和l外一点A.
求作:点A关于l的对称点A'.
作法:①在l上任取一点P,以点P为圆心,PA长为半径作孤,交l于点B;②以点B为圆心,AB长为半径作弧,交弧AB于点A'. 点A'就是所求作的对称点.
由步骤①,得________
由步骤②,得________
将横线上的内容填写完整,并说明点A与A'关于直线l对称的理由________.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县某包装生产企业承接了一批上海世博会的礼品盒制作业务,为了确保质量,该企业进行试生产.他们购得规格是![]() 的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下
的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下![]() 型与
型与![]() 型两种板材.如图甲所示.(单位
型两种板材.如图甲所示.(单位![]() )
)
(1)列出方程(组),求出图甲中![]() 与
与![]() 的值;
的值;
(2)在试生产阶段,若将625张标准板材用裁法一裁剪,125张标准板材用裁法二裁剪,再将得到的![]() 型与
型与![]() 型板材做侧面和底面,刚好可以做成图乙的竖式与横式两种无盖礼品盒.求可以做竖式与横式两种无盖礼品盒各多少个?
型板材做侧面和底面,刚好可以做成图乙的竖式与横式两种无盖礼品盒.求可以做竖式与横式两种无盖礼品盒各多少个?


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“品中华诗词,寻文化自信”.某校组织全校1000名学生举办了第二届“中华诗词大赛”的初赛,从中抽取部分学生的成绩统计后,绘制了如下不完整的频数分布统计表与频数分布直方图.
频数分布统计表
组别 | 成绩 | 人数 | 百分比 |
|
| 8 | 20% |
|
| 16 |
|
|
|
| 30% |
|
| 4 | 10% |
频数分布直方图

请观察图表,解答下列问题:
(1)表中![]() __________,
__________,![]() __________;
__________;
(2)补全频数分布直方图;
(3)如果成绩达到90及90分以上者为优秀,可推荐参加决赛,那么请你估计该校进入决赛的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果mx+n=0,其中m、n为有理数,x为无理数,那么m=0且n=0.
(1)如果![]() ,其中a、b为有理数,那么a= ,b= .
,其中a、b为有理数,那么a= ,b= .
(2)如果![]() ,其中a、b为有理数,求a+2b的值.
,其中a、b为有理数,求a+2b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
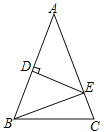
【题目】(3分)如图,△ABC中,AB=AC,AB的垂直平分线交边AB于D点,交边AC于E点,若△ABC与△EBC的周长分别是40cm,24cm,则AB= cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)①如图①![]() 的内角
的内角![]() 的平分线与内角
的平分线与内角![]() 的平分线相交于
的平分线相交于![]() 点,请探究
点,请探究![]() 与
与![]() 的关系,并说明理由.
的关系,并说明理由.
②如图②,![]() 的内角
的内角![]() 的平分线与外角
的平分线与外角![]() 的平分线相交于
的平分线相交于![]() 点,请探究
点,请探究![]() 与
与![]() 的关系,并说明理由.
的关系,并说明理由.
(2)如图③④,四边形![]() 中,设
中,设![]() ,
,![]() ,
,![]() 为四边形
为四边形![]() 的内角
的内角![]() 与外角
与外角![]() 的平分线所在直线相交而行成的锐角.请利用(1)中的结论完成下列问题:
的平分线所在直线相交而行成的锐角.请利用(1)中的结论完成下列问题:
①如图③,求![]() 的度数.(用
的度数.(用 ![]() 的代数式表示)
的代数式表示)
②如图④,将四边形![]() 沿着直线
沿着直线![]() 翻折得到四边形
翻折得到四边形![]() ,
,![]() 为
为![]() 延长线上一点,连接
延长线上一点,连接![]() ,
,![]() 与
与![]() 的角平分线交于点
的角平分线交于点![]() ,求
,求![]() 与
与![]() 的数量关系.
的数量关系.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】盒中有x枚黑棋和y枚白棋,这些棋除颜色外无其他差别.
(1)从盒中随机取出一枚棋子,如果它是黑棋的概率是![]() ,写出表示x和y关系的表达式.
,写出表示x和y关系的表达式.
(2)往盒中再放进10枚黑棋,取得黑棋的概率变为![]() ,求x和y的值.
,求x和y的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com