
科目:初中数学 来源:2016-2017学年湖北省武汉市侏儒山街四校八年级3月月考数学试卷(解析版) 题型:单选题
在下列长度的各组线段中,能构成直角三角形的是()
A. 3,5,9 B. 1, 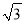 ,2
,2
C. 4,6,8 D. 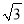 ,
, 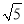 ,
, 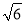
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 所谓气质,是指婴儿出生后最早表示出来的以一种较为明显而稳定的人格特征类型,也指孩子对身体内在或外来刺激反应的方式.心理学界常将气质分为四大类:胆汁型、多血质、黏液质、抑郁质.我校心理协会为了更好的了解学生,在高中随机发放了若干份问卷调查,并将统计结果绘制成如图表:
所谓气质,是指婴儿出生后最早表示出来的以一种较为明显而稳定的人格特征类型,也指孩子对身体内在或外来刺激反应的方式.心理学界常将气质分为四大类:胆汁型、多血质、黏液质、抑郁质.我校心理协会为了更好的了解学生,在高中随机发放了若干份问卷调查,并将统计结果绘制成如图表:| 气质类型 | 频数 | 频率 |
| 胆汁型 | 180 | a |
| 多血质 | 140 | 0.28 |
| 黏液质 | 80 | 0.16 |
| 抑郁质 | b | 0.20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com