
分析 (1)直接利用完全平方公式结合已知变形得出答案;
(2)利用完全平方公式分解因式即可;
(3)首先将原式利用完全平方公式分解因式,进而得出答案.
解答 解:(1)x2-4x+1=(x-2)2-3,x2-4x+1=(x-1)2-2x,
x2-4x+1=(2x-1)2-3x2;
(2)x4+x2y2+y4
=x4+2x2y2+y4-x2y2,
=(x2+y2)2-x2y2,
=(x2+y2+xy)(x2+y2-xy);
(3)∵a2+b2+c2=ab+3b+2c-4,
∴(a-$\frac{1}{2}$b)2+$\frac{3}{4}$(b-2)2+(c-1)2=0,
故b=2,c=1,a=1,
则a+b+c=4.
点评 此题主要考查了因式分解的应用,正确应用乘法公式是解题关键.


科目:初中数学 来源: 题型:解答题
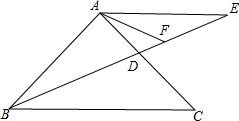 如图,已知等腰△ABC中,AB=AC,点D是AC上一动点,点E在BD的延长线上,且AB=AE,AF平分∠CAE,交DE于F,∠ABC=45°,且BD平分∠ABC,请你证明,BD=2FE.
如图,已知等腰△ABC中,AB=AC,点D是AC上一动点,点E在BD的延长线上,且AB=AE,AF平分∠CAE,交DE于F,∠ABC=45°,且BD平分∠ABC,请你证明,BD=2FE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 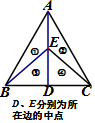 | B. | 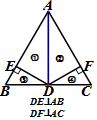 | C. | 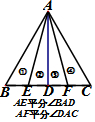 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
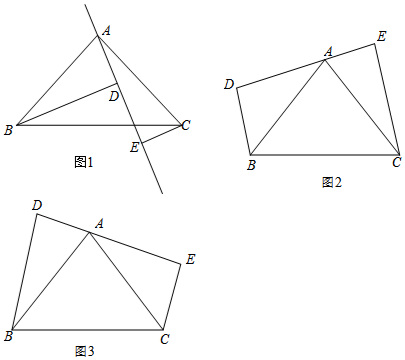
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{x+1}{|x|}$ | B. | $\frac{x+1}{{x}^{2}}$ | C. | $\frac{x+1}{{x}^{2}+1}$ | D. | $\frac{x+1}{{x}^{2}-4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,⊙O的半径为1,点A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.
如图,⊙O的半径为1,点A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com