
 如图,⊙O的半径为1,点A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.
如图,⊙O的半径为1,点A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.分析 (1)利用圆周角定理可得∠BAC=∠CPB,∠ABC=∠APC,而∠APC=∠CPB=60°,所以∠BAC=∠ABC=60°,证明△ABC是等边三角形;
(2)在PC上截取PD=AP,则△APD是等边三角形,然后证明△APB≌△ADC,证明BP=CD,即可证得;
(3)过点P作PE⊥AB,垂足为E,过点C作CF⊥AB,垂足为F,把四边形的面积转化为两个三角形的面积进行计算,当点P为$\widehat{AB}$的中点时,PE+CF=PC从而得出最大面积.
解答 (1)在⊙O中,∠BAC与∠CPB是$\widehat{BC}$所对的圆周角,∠ABC与∠APC是$\widehat{AC}$所对的圆周角,
∴∠BAC=∠CPB,∠ABC=∠APC,
∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∴△ABC为等边三角形;
故答案为:等边三角形;
(2)①如图1,在PC上截取PD=AP,
又∵∠APC=60°,
∴△APD是等边三角形,
∴AD=AP=PD,∠ADP=60°,即∠ADC=120°.
又∵∠APB=∠APC+∠BPC=120°,
∴∠ADC=∠APB,
在△APB和△ADC中,
$\left\{\begin{array}{l}{∠ABP=∠ACD}\\{∠APB=∠ADC}\\{AP=AD}\end{array}\right.$,
∴△APB≌△ADC(AAS),
∴BP=CD,
又∵PD=AP,
∴CP=BP+AP,
故答案为:CP=BP+AP;
②当点P为$\widehat{AB}$的中点时,四边形APBC的面积最大.
理由如下,如图2,过点P作PE⊥AB,垂足为E.
过点C作CF⊥AB,垂足为F.
∵S△APB=$\frac{1}{2}$AB•PE,S△ABC=$\frac{1}{2}$AB•CF,
∴S四边形APBC=$\frac{1}{2}$AB•(PE+CF),
当点P为$\widehat{AB}$的中点时,PE+CF=PC,PC为⊙O的直径
∴此时四边形APBC的面积最大.
又∵⊙O的半径为1,
∴其内接正三角形的边长AB=$\sqrt{3}$,
∴S四边形APBC=$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$.,
故答案为:$\sqrt{3}$.
点评 本题考查了圆周角定理、等边三角形的判定、三角形的面积公式以及三角形的全等的判定与性质,正确作出辅助线,证明△APB≌△ADC是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
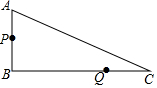 如图,在Rt△ABC中,∠B=90°,AB=7cm,AC=25cm.点P从点A沿AB方向以1cm/s的速度运动至点B,点Q从点B沿BC方向以6cm/s的速度运动至点C,P、Q两点同时出发.
如图,在Rt△ABC中,∠B=90°,AB=7cm,AC=25cm.点P从点A沿AB方向以1cm/s的速度运动至点B,点Q从点B沿BC方向以6cm/s的速度运动至点C,P、Q两点同时出发.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
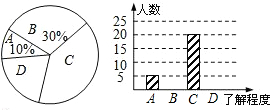
 所谓气质,是指婴儿出生后最早表示出来的以一种较为明显而稳定的人格特征类型,也指孩子对身体内在或外来刺激反应的方式.心理学界常将气质分为四大类:胆汁型、多血质、黏液质、抑郁质.我校心理协会为了更好的了解学生,在高中随机发放了若干份问卷调查,并将统计结果绘制成如图表:
所谓气质,是指婴儿出生后最早表示出来的以一种较为明显而稳定的人格特征类型,也指孩子对身体内在或外来刺激反应的方式.心理学界常将气质分为四大类:胆汁型、多血质、黏液质、抑郁质.我校心理协会为了更好的了解学生,在高中随机发放了若干份问卷调查,并将统计结果绘制成如图表:| 气质类型 | 频数 | 频率 |
| 胆汁型 | 180 | a |
| 多血质 | 140 | 0.28 |
| 黏液质 | 80 | 0.16 |
| 抑郁质 | b | 0.20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com