
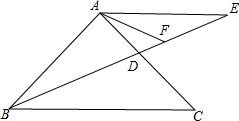
 如图,已知等腰△ABC中,AB=AC,点D是AC上一动点,点E在BD的延长线上,且AB=AE,AF平分∠CAE,交DE于F,∠ABC=45°,且BD平分∠ABC,请你证明,BD=2FE.
如图,已知等腰△ABC中,AB=AC,点D是AC上一动点,点E在BD的延长线上,且AB=AE,AF平分∠CAE,交DE于F,∠ABC=45°,且BD平分∠ABC,请你证明,BD=2FE. 分析 连接CF,延长BA、CF交N,首先证明△ACF≌△AEF(SAS),推出CF=EF,再证△BFC≌△BFN,推出CN=2CF=2EF,证△BAD≌△CAN,推出BD=CN,即可得出答案.
解答 证明:连接CF,延长BA、CF交N,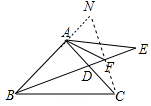
∵AF平分∠CAE,
∴∠EAF=∠CAF,
∵AB=AC,AB=AE,
∴AE=AC,
在△ACF和△AEF中,
$\left\{\begin{array}{l}{AE=AC}\\{∠EAF=∠CAF}\\{AF=AF}\end{array}\right.$,
∴△ACF≌△AEF(SAS),
∴CF=EF
∵∠ABC=45°,BD平分∠ABC,AB=AC,
∴∠ABF=∠CBF=22.5°,∠ACB=45°,∠BAC=180°-45°-45°=90°,
∴∠ACF=∠ABF=22.5°,
∴∠BFC=180°-22.5°-45°-22.5°=90°,
∴∠BFN=∠BFC=90°,
在△BFN和△BFC中
$\left\{\begin{array}{l}{∠NBF=∠CBF}\\{BF=BF}\\{∠BFN=∠BFC}\end{array}\right.$,
∴△BFN≌△BFC(ASA),
∴CF=FN,
即CN=2CF=2EF,
∵∠BAC=90°,
∴∠NAC=∠BAD=90°,
在△BAD和△CAN中
$\left\{\begin{array}{l}{∠ABD=∠ACN}\\{AB=AC}\\{∠BAD=∠CAN}\end{array}\right.$,
∴△BAD≌△CAN(ASA),
∵CF=EF
∴BD=CN=2CF=2EF.
点评 本题考查了等腰直角三角形性质和判定,全等三角形的性质和判定,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.


科目:初中数学 来源:2016-2017学年湖北省武汉市侏儒山街四校八年级3月月考数学试卷(解析版) 题型:单选题
在下列长度的各组线段中,能构成直角三角形的是()
A. 3,5,9 B. 1, 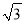 ,2
,2
C. 4,6,8 D. 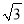 ,
, 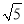 ,
, 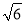
查看答案和解析>>
科目:初中数学 来源:2016-2017学年湖北省枝江市八年级3月调研考试数学试卷(解析版) 题型:单选题
△ABC中,AB=13cm,AC=15cm,高AD=12,则BC的长为( )
A. 14 B. 4 C. 14或4 D. 以上都不对
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
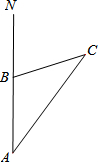 如图,上午9时,一条船从A处出发,以20海里/时的速度向正北航行,12时到达B处,测得∠NAC=36°,∠ABC=108°,求从B处到灯塔C的距离.
如图,上午9时,一条船从A处出发,以20海里/时的速度向正北航行,12时到达B处,测得∠NAC=36°,∠ABC=108°,求从B处到灯塔C的距离.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com