
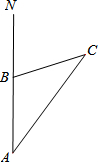
 如图,上午9时,一条船从A处出发,以20海里/时的速度向正北航行,12时到达B处,测得∠NAC=36°,∠ABC=108°,求从B处到灯塔C的距离.
如图,上午9时,一条船从A处出发,以20海里/时的速度向正北航行,12时到达B处,测得∠NAC=36°,∠ABC=108°,求从B处到灯塔C的距离.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2017届湖北省襄阳市九年级下学期第一次月考数学试卷(解析版) 题型:单选题
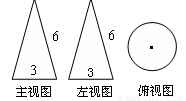
一个几何体的三视图如图,其中主视图都是腰长为6、底边长为3的等腰三角形,则这个几何体的侧面展开图的面积为( )
A. 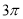 B.
B. 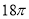 C.
C. 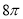 D.
D. 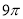
查看答案和解析>>
科目:初中数学 来源:2016-2017学年湖北省武汉市侏儒山街四校八年级3月月考数学试卷(解析版) 题型:单选题
要使式子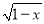 有意义,则x的取值范围是()
有意义,则x的取值范围是()
A. x≤1 B. x≥1 C. x>0 D. x>﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
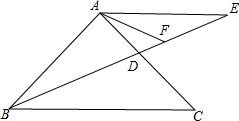 如图,已知等腰△ABC中,AB=AC,点D是AC上一动点,点E在BD的延长线上,且AB=AE,AF平分∠CAE,交DE于F,∠ABC=45°,且BD平分∠ABC,请你证明,BD=2FE.
如图,已知等腰△ABC中,AB=AC,点D是AC上一动点,点E在BD的延长线上,且AB=AE,AF平分∠CAE,交DE于F,∠ABC=45°,且BD平分∠ABC,请你证明,BD=2FE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在四边形ABCD中,AB∥CD,AD=BC,∠A=∠B=90°,E是AB上一点,且DE=DC,过点C作CF⊥DE,垂足为点F.
如图所示,在四边形ABCD中,AB∥CD,AD=BC,∠A=∠B=90°,E是AB上一点,且DE=DC,过点C作CF⊥DE,垂足为点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
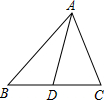 如图,在△ABC中,AC=5,中线AD=7,则AB边的取值范围是( )
如图,在△ABC中,AC=5,中线AD=7,则AB边的取值范围是( )| A. | 1<AB<29 | B. | 4<AB<24 | C. | 5<AB<19 | D. | 9<AB<19 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{x+1}{|x|}$ | B. | $\frac{x+1}{{x}^{2}}$ | C. | $\frac{x+1}{{x}^{2}+1}$ | D. | $\frac{x+1}{{x}^{2}-4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com