
【题目】若顺次连接四边形ABCD四边中点形成的四边形为矩形,则四边形ABCD满足的条件为.___________
【答案】AC⊥BD
【解析】
如图所示,由四边形EFGH为矩形,根据矩形的四个角为直角得到∠FEH=90°,又EF为三角形ABD的中位线,根据中位线定理得到EF与DB平行,根据两直线平行,同旁内角互补得到∠EMO=90°,同理根据三角形中位线定理得到EH与AC平行,再根据两直线平行,同旁内角互补得到∠AOD=90°,根据垂直定义得到AC与BD垂直.
顺次连接四边形ABCD四边中点形成的四边形为矩形,则四边形ABCD满足的条件为对角线垂直,理由:
∵四边形EFGH是矩形,
∴∠FEH=90°,
又∵点E、F、分别是AD、AB、各边的中点,
∴EF是三角形ABD的中位线,
∴EF∥BD,
∴∠FEH=∠OMH=90°,
又∵点E、H分别是AD、CD各边的中点,
∴EH是三角形ACD的中位线,
∴EH∥AC,
∴∠OMH=∠COB=90°,
则AC⊥BD,故四边形ABCD满足的条件为对角线垂直.
故答案为:AC⊥BD.



科目:初中数学 来源: 题型:
【题目】如图,![]() 中,AB=AC,D、E分别在边AB、AC上,且满足AD=AE.下列结论中:①
中,AB=AC,D、E分别在边AB、AC上,且满足AD=AE.下列结论中:①![]() ;②AO平分∠BAC;③OB=OC;④AO⊥BC;⑤若
;②AO平分∠BAC;③OB=OC;④AO⊥BC;⑤若![]() ,则
,则![]() ;其中正确的有( )
;其中正确的有( )

A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学骑自行车去郊外春游,骑行1小时后,自行车出现故障,维修好后继续骑行,下图表示他离家的距离y(千米)与所用的时间x(时)之间关系的图象.
(1)根据图象回答:小明到达离家最远的地方用了多长时间?此时离家多远?
(2)求小明出发2.5小时后离家多远;
(3)求小明出发多长时间离家12千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在![]() 中,
中,![]() 于
于![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() ,求
,求![]() 和
和![]() 的度数.对于上述问题,在以下解答过程的空白处填上适当的内容(理由或数学式).
的度数.对于上述问题,在以下解答过程的空白处填上适当的内容(理由或数学式).
解:∵![]() ,
,![]() 平分
平分![]() (______)
(______)
∴![]() ______
______![]() ______
______![]() ______.(角平分线的定义)
______.(角平分线的定义)
∵![]() (已知)
(已知)
∴![]() ______
______![]() ______
______![]() ______.(______)
______.(______)
∵![]() (______)
(______)
∴![]() (等式的性质)
(等式的性质)
![]() ______(等量代换)
______(等量代换)
![]() ______.
______.
∵![]() 于
于![]() (已知)
(已知)
∴![]() (______)
(______)
在直角三角形![]() 中,
中,
∵![]() (______)
(______)
∴![]() (等式的性质)
(等式的性质)
![]() ______(等量代换)
______(等量代换)
![]() ______.
______.

查看答案和解析>>
科目:初中数学 来源: 题型:
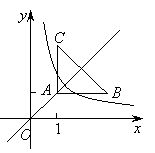
【题目】如图:等腰直角三角形ABC位于第一象限,AB=AC=2,直角顶点A在直线y=x上,其中A点的横坐标为1,且两条直角边AB、AC分别平行于x轴、y轴,若双曲线![]() (k≠0)与
(k≠0)与![]() 有交点,则k的取值范围是( )
有交点,则k的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
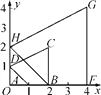
【题目】如图,在平面直角坐标系中,四边形ABCD的各顶点坐标分别为A(1,0),B(2,0),C(2,2),D(0,1),四边形BFGH的各顶点坐标分别为F(4,0),G(4,4),H(0,2),则下列说法正确的是( )
A. 四边形ABCD与四边形BFGH相似但不位似
B. 四边形ABCD与四边形BFGH位似但不相似
C. 四边形ABCD与四边形BFGH位似,且相似比为1∶![]()
D. 四边形ABCD与四边形BFGH位似,且相似比为1∶2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一块木板如图所示,已知AB=4,BC=3,DC=12,AD=13,∠B=90°,木板的面积为( )

A. 60 B. 30 C. 24 D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是BC上的一点,连接AE,作BF⊥AE,垂足为H,交CD于F,作CG∥AE,交BF于G.
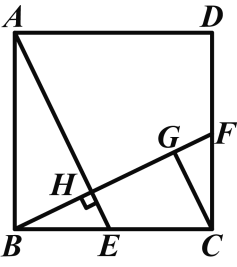
求证:(1)CG=BH;
(2)FC2=BF·GF;
(3)![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com