练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．已知0＜x＜1，且x+$\frac{1}{x}$=$\sqrt{8}$，求x-$\frac{1}{x}$的值．

    分析 把已知等式两边平方，利用完全平方公式化简，整理求出x2+$\frac{1}{{x}^{2}}$的值，原式平方，利用完全平方公式化简，开方即可求出值．

    解答 解：∵0＜x＜1，且x+$\frac{1}{x}$=$\sqrt{8}$，
    ∴（x+$\frac{1}{x}$）2=x2+$\frac{1}{{x}^{2}}$+2=8，即x2+$\frac{1}{{x}^{2}}$=6，x-$\frac{1}{x}$＜0，
    ∴（x-$\frac{1}{x}$）2=x2+$\frac{1}{{x}^{2}}$-2=4，
    则x-$\frac{1}{x}$=-2．

    点评 此题考查了完全平方公式，熟练掌握完全平方公式是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    13．“抢红包”是2015年春节十分火爆的一项网络活动，某企业有4000名职工，从中随机抽取350人，按年龄分布和对“抢红包”所持态度情况进行了调查，并将调查结果绘成了条形统计图和扇形统计图．

    （1）这次调查中，如果职工年龄的中位数是整数，那么这个中位数所在的年龄段是哪一段？
    （2）如果把对“抢红包”所持态度中的“经常（抢红包）”和“偶尔（抢红包）”统称为“参与抢红包”，那么这次接受调查的职工中“参与抢红包”的人数是多少？
    （3）请估计该企业“从不（抢红包）”的人数是多少？

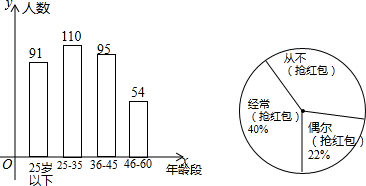
    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

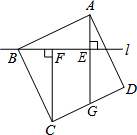    14．如图，过正方形ABCD的顶点B作直线l，过点A，C作直线l的垂线，垂足分别为E，F，直线AE交CD于点G．
    （1）求证：△ABE≌△BCF；
    （2）若∠CBF=65°，求∠AGC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．我们把能二等分多边形面积的直线称为多边形的“好线”，请用无刻度的直尺作出图（1）、图（2）的“好线”．其中图（1）是一个平行四边形，图（2）由一个平行四边形和一个正方形组成．（保留作图痕迹，不写作法）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．如图，线段AC与BD相交于点O，连接AB，CD，若AB∥CD，BO=DO，AF=CE．
    （1）请说明点O是AC的中点；
    （2）猜想BE与DF的数量关系和位置关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．若n为正整数，试说明3n+3-4n+1+3n+1-22n能被10整除．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

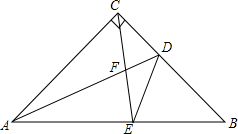    15．如图，在等腰Rt△ABC中，∠ACB=90°，AC=BC，D为BC的中点，E为斜边AB上一点，且AE=2EB，CE与AD交于点F，连接DE．
    （1）求AF：FD；
    （2）求证：CE⊥AD；
    （3）求证：∠ADC=∠BDE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    12．点A（-4，y1）和B（-3，y2）都在直线y=$\frac{1}{2}$x上，则y1与y2的关系是y1＞y2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．将x4-2x2+1因式分解的最终结果是（x-1）2（x+1）2．

    查看答案和解析>>

    同步练习册答案