
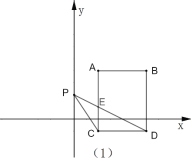
【题目】在平面直角坐标系中,已知点![]() ,
,![]() ,连接
,连接![]() ,将
,将![]() 向下平移5个单位得线段
向下平移5个单位得线段![]() ,其中点
,其中点![]() 的对应点为点
的对应点为点![]() .
.
(1)填空:点![]() 的坐标为_________,线段
的坐标为_________,线段![]() 平移到
平移到![]() 扫过的面积为_______;
扫过的面积为_______;
(2)若点![]() 是
是![]() 轴上的动点,连接
轴上的动点,连接![]() .
.
①如图(1),当点![]() 在
在![]() 轴正半轴时,线段
轴正半轴时,线段![]() 与线段
与线段![]() 相交于点
相交于点![]() ,用等式表示三角形
,用等式表示三角形![]() 的面积与三角形
的面积与三角形![]() 的面积之间的关系,并说明理由;
的面积之间的关系,并说明理由;
②当![]() 将四边形
将四边形![]() 的面积分成
的面积分成![]() 两部分时,求点
两部分时,求点![]() 的坐标.
的坐标.

【答案】(1)![]() ,20;(2)①
,20;(2)①![]() ;理由见解析;②
;理由见解析;②![]() 或
或![]() .
.
【解析】
(1)由平移的性质得出点C坐标,AC=5,再求出AB,即可得出结论;
(2)①先求出PF=2,再用三角形的面积公式得出S△PEC=CE,S△ECD=2CE,即可得出结论;
②分DP交线段AC和交AB两种情况,利用面积之差求出△PCE和△PBE,最后用三角形面积公式即可得出结论.
(1)∵点A(2,4),将AB向下平移5个单位得线段CD,
∴C(2,45),
即:C(2,1),
由平移得,AC=5,四边形ABDC是矩形,
∵A(2,4),B(6,4),
∴AB=62=4,
∴S四边形ABDC=ABAC=4×5=20,
即:线段AB平移到CD扫过的面积为20,
故答案为:(2,1),20;
(2)①过P点作PF⊥AC于F,
由平移知,AC∥y轴,
∵A(2,4),PF=2
由平移知,CD=AB=4,
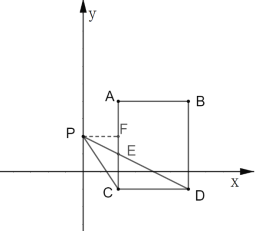
∴![]()
又∵![]()
∴![]()
②如图2,当PD交线段AC于E,且PD将四边形ACDB分成面积为2:3两部分时,
连结PC,延长DC交y轴于点M,则M(0,1),
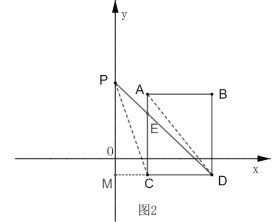
∴OM=1,
连接AD,则S△ACD=![]() S矩形ABDC=10,
S矩形ABDC=10,
∵PD将四边形ACDB的面积分成2:3两部分,
∴S△CDE=![]() S矩形ABDC=
S矩形ABDC=![]() ×20=8,
×20=8,
由①知,S△PEC=![]() S△ECD=
S△ECD=![]() ×8=4
×8=4
∴/span>S△PCD=S△PEC+S△ECD=4+8=12,
∵S△PCD=![]() CDPM=
CDPM=![]() ×4PM=12,
×4PM=12,
∴PM=6,
∴PO=PMOM=61=5,
∴P(0,5).
(ⅱ)如图3,当PD交AB于点F,PD将四边形ACDB分成面积为2:3两部分时,
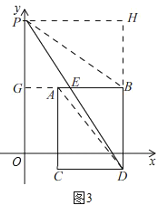
连结PB,延长BA交y轴于点G,则G(0,4),
∴OG=4,
连接AD,则S△ABD=![]() S矩形ABDC=10,
S矩形ABDC=10,
∵PD将四边形ACDB的面积分成2:3两部分,
∴S△BDE=![]() S矩形ABDC=
S矩形ABDC=![]() ×20=8,
×20=8,
∵S△BDE=![]() BDBE=
BDBE=![]() ×5BE=8,
×5BE=8,
∴BE=![]()
过P点作PH⊥BD交DB的延长线于点H,
∵B(6,4),
∴PH=6
S△PDB=![]() BD×PH=
BD×PH=![]() ×5×6=15,
×5×6=15,
∴S△PBE=S△PDBS△BDE=158=7,
∵S△PBE=![]() BEPG=
BEPG=![]() ×
×![]() PG=7,
PG=7,
∴PG=![]() ,
,
∴PO=PG+OG=![]() +4=
+4=![]() ,
,
∴P(0,![]() ),
),
综上所述,![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
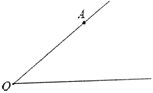
【题目】如图,点![]() 在
在![]() 的一边
的一边![]() 上,按要求画图并填空:
上,按要求画图并填空:
(1)过点![]() 画直线
画直线![]() ,与
,与![]() 的另一边相交于点
的另一边相交于点![]() ;
;
(2)过点![]() 画
画![]() 的垂线
的垂线![]() ,垂足为点
,垂足为点![]() ;
;
(3)过点![]() 画直线
画直线![]() ,交直线
,交直线![]() 于点
于点![]() ;
;
(4)直接写出![]() _____
_____![]() ;
;
(5)如果![]() ,
,![]() ,
,![]() ,那么点
,那么点![]() 到直线
到直线![]() 的距离为_______.
的距离为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
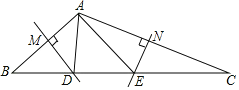
(1)若BC=8,则△ADE周长是多少?
(2)若∠BAC=118°,则∠DAE的度数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD⊥BC于点D,且BD=DC,E是BC延长线上一点,且点C在AE的垂直平分线上.有下列结论:
①AB=AC=CE;②AB+BD=DE;③AD=![]() AE;④BD=DC=CE.
AE;④BD=DC=CE.
其中,正确的结论是( )

A. 只有![]() B. 只有
B. 只有![]()
C. 只有![]() D. 只有
D. 只有![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD对角线BD上截取BE=BC,连接CE并延长交AD于点F,连接AE,过B作BG⊥AE于点G,交AD于点H,则下列结论错误的是( )
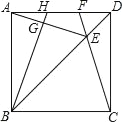
A. AH=DF B. S四边形EFHG=S△DCF+S△AGH
C. ∠AEF=45° D. △ABH≌△DCF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(1,2)、点 B在双曲线y= ![]() (x>0)上,过B作BC⊥x轴于点C,如图,P是y轴上一点,
(x>0)上,过B作BC⊥x轴于点C,如图,P是y轴上一点,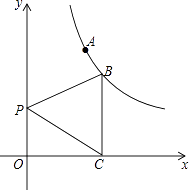
(1)求k的值及△PBC的面积;
(2)设点M(x1 , y1)、N(x2 , y2)(x2>x1>0)是双曲线y= ![]() (x>0)上的任意两点,s=
(x>0)上的任意两点,s= ![]() ,t=
,t= ![]() ,试判断s与t的大小关系,并说明理由.
,试判断s与t的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用图1,图2提供的某公司的一些信息,解答下列问题.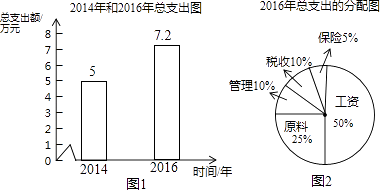
(1)2016年该公司工资支出的金额是万元;
(2)2014年到2016年该公司总支出的年平均增长率;
(3)若保持这种增长速度,请你预估该公司2017年的总支出.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com