
【题目】已知点A(1,2)、点 B在双曲线y= ![]() (x>0)上,过B作BC⊥x轴于点C,如图,P是y轴上一点,
(x>0)上,过B作BC⊥x轴于点C,如图,P是y轴上一点,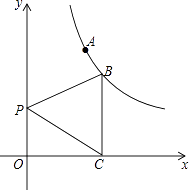
(1)求k的值及△PBC的面积;
(2)设点M(x1 , y1)、N(x2 , y2)(x2>x1>0)是双曲线y= ![]() (x>0)上的任意两点,s=
(x>0)上的任意两点,s= ![]() ,t=
,t= ![]() ,试判断s与t的大小关系,并说明理由.
,试判断s与t的大小关系,并说明理由.
【答案】
(1)解:把A(1,2)代入y= ![]() 得k=2;
得k=2;
设B的坐标是(m,n)则mn=2,BC=n,OC=m.
则S△PBC= ![]() BCOC=
BCOC= ![]() mn=1
mn=1
(2)解:s>t;
理由:∵s﹣t= ![]()
═ ![]()
═ ![]() =
= ![]() ,
,
∵x2>x1>0,
∴ ![]() >0,x1x2(x1+x2)>0,
>0,x1x2(x1+x2)>0,
∴ ![]() ;
;
∴s>t
【解析】(1)利用待定系数法即可求得k的值;设B的坐标是(m,n)则mn=2,BC=n,OC=m,利用三角形的面积公式求解;(2)把y1和y2用x1和x2,然后求s﹣t得值,对式子进行变形判断s﹣t的符号即可。
【考点精析】解答此题的关键在于理解比例系数k的几何意义的相关知识,掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2﹣2bx+c,当x<2时,y的值随x的增大而增大,则实数b的取值范围是( )
A.b≥﹣1
B.b≤﹣1
C.b≥﹣2
D.b≤﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点![]() ,
,![]() ,连接
,连接![]() ,将
,将![]() 向下平移5个单位得线段
向下平移5个单位得线段![]() ,其中点
,其中点![]() 的对应点为点
的对应点为点![]() .
.
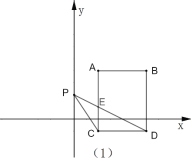
(1)填空:点![]() 的坐标为_________,线段
的坐标为_________,线段![]() 平移到
平移到![]() 扫过的面积为_______;
扫过的面积为_______;
(2)若点![]() 是
是![]() 轴上的动点,连接
轴上的动点,连接![]() .
.
①如图(1),当点![]() 在
在![]() 轴正半轴时,线段
轴正半轴时,线段![]() 与线段
与线段![]() 相交于点
相交于点![]() ,用等式表示三角形
,用等式表示三角形![]() 的面积与三角形
的面积与三角形![]() 的面积之间的关系,并说明理由;
的面积之间的关系,并说明理由;
②当![]() 将四边形
将四边形![]() 的面积分成
的面积分成![]() 两部分时,求点
两部分时,求点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个运算程序:

例如:根据所给的运算程序可知,当![]() 时,
时,![]() ,再把
,再把![]() 代入,得
代入,得![]() ,则输出的结果为
,则输出的结果为![]() .
.
(1)当![]() 时,输出的结果为_________;当
时,输出的结果为_________;当![]() 时,输出结果为_________;
时,输出结果为_________;
(2)若需要经过两次运算才能输出结果,![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了倡导节能低碳的生活,某公司对集体宿舍用电收费作如下规定:一间宿舍一个月用电量不超过a千瓦时,则一个月的电费为20元;若超过a千瓦时,则除了交20元外,超过部分每千瓦时要交 ![]() 元.某宿舍3月份用电80千瓦时,交电费35元;4月份用电45千瓦时,交电费20元.
元.某宿舍3月份用电80千瓦时,交电费35元;4月份用电45千瓦时,交电费20元.
(1)求a的值;
(2)若该宿舍5月份交电费45元,那么该宿舍当月用电量为多少千瓦时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图A在数轴上所对应的数为﹣2.
(1)点B在点A右边距A点4个单位长度,求点B所对应的数;
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点 B 以每秒2个单位长度沿数轴向右运动,当点A运动到﹣6所在的点处时,求A,B两点间距离.
(3)在(2)的条件下,现A点静止不动,B点再以每秒2个单位长度沿数轴向左运动时,经过多长时间A,B两点相距4个单位长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了激发学生爱数学、学数学、用数学的热情,某学校在七年级开展“魅力数学”趣味竞赛,该校七年级共有学生400人参加竞赛.现随机抽取40名参赛学生的成绩数据(百分制)进行整理、描述和分析.
74 97 96 89 98 74 69 76 72 78
99 72 97 76 99 74 99 73 98 74
76 88 93 65 78 94 89 68 95 50
89 88 89 89 77 94 87 88 92 91
范围 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
频数 | 1 | m | 13 | 9 | 14 |
平均数、中位数、众数如下表所示:
平均数 | 中位数 | 众数 |
84.1 | n | 89 |
根据以上信息,回答下列问题:
(1)m= ,n= ;
(2)小明说:“这次竞赛我得了84分,在所有参赛学生中排名属中等偏上!”小明的说法 (填“正确”或“不正确”),理由是 ;
(3)若成绩不低于85分可以进入决赛,估计参赛的400名学生中能进入决赛的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办八年级学生数学素养大赛,比赛共设四个项目:七巧板拼图,趣题巧解,数学应用,魔方复原,每个项目得分都按一定百分比折算后记入总分,下表为甲,乙,丙三位同学得分情况(单位:分)
七巧板拼图 | 趣题巧解 | 数学应用 | 魔方复原 | |
甲 | 66 | 89 | 86 | 68 |
乙 | 66 | 60 | 80 | 68 |
丙 | 66 | 80 | 90 | 68 |
(1)比赛后,甲猜测七巧板拼图,趣题巧解,数学应用,魔方复原这四个项目得分分别按10%,40%,20%,30%折算△记入总分,根据猜测,求出甲的总分;
(2)本次大赛组委会最后决定,总分为80分以上(包含80分)的学生获一等奖,现获悉乙,丙的总分分别是70分,80分.甲的七巧板拼图、魔方复原两项得分折算后的分数和是20分,问甲能否获得这次比赛的一等奖?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com