
【题目】为了激发学生爱数学、学数学、用数学的热情,某学校在七年级开展“魅力数学”趣味竞赛,该校七年级共有学生400人参加竞赛.现随机抽取40名参赛学生的成绩数据(百分制)进行整理、描述和分析.
74 97 96 89 98 74 69 76 72 78
99 72 97 76 99 74 99 73 98 74
76 88 93 65 78 94 89 68 95 50
89 88 89 89 77 94 87 88 92 91
范围 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
频数 | 1 | m | 13 | 9 | 14 |
平均数、中位数、众数如下表所示:
平均数 | 中位数 | 众数 |
84.1 | n | 89 |
根据以上信息,回答下列问题:
(1)m= ,n= ;
(2)小明说:“这次竞赛我得了84分,在所有参赛学生中排名属中等偏上!”小明的说法 (填“正确”或“不正确”),理由是 ;
(3)若成绩不低于85分可以进入决赛,估计参赛的400名学生中能进入决赛的人数.
【答案】(1)m=3,n=88;(2)不正确,中位数为88,84<88;(3)230.
【解析】
(1)用40减去各个范围的人数可求m,这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.
(2)小明得了84分,略低于竞赛成绩样本数据的中位数88,说明小亮的成绩排名属中等偏下.
(3)根据竞赛成绩不低于85分的人数为17,即可估计参赛的400名学生中能进入决赛的人数.
(1)m=40﹣1﹣13﹣9﹣14=3,
从小到大排列,第20和21个数都是88,中位数n=88;
(2)小明说:“这次竞赛我得了84分,在所有参赛学生中排名属中等偏上!”
小明的说法 不正确,理由是 中位数为88,84<88;
(3)400×![]() =230(人).
=230(人).
故估计参赛的400名学生中能进入决赛的人数为230人.
故答案为:3;88;不正确;中位数为88,84<88.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
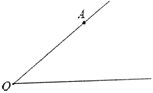
【题目】如图,点![]() 在
在![]() 的一边
的一边![]() 上,按要求画图并填空:
上,按要求画图并填空:
(1)过点![]() 画直线
画直线![]() ,与
,与![]() 的另一边相交于点
的另一边相交于点![]() ;
;
(2)过点![]() 画
画![]() 的垂线
的垂线![]() ,垂足为点
,垂足为点![]() ;
;
(3)过点![]() 画直线
画直线![]() ,交直线
,交直线![]() 于点
于点![]() ;
;
(4)直接写出![]() _____
_____![]() ;
;
(5)如果![]() ,
,![]() ,
,![]() ,那么点
,那么点![]() 到直线
到直线![]() 的距离为_______.
的距离为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(1,2)、点 B在双曲线y= ![]() (x>0)上,过B作BC⊥x轴于点C,如图,P是y轴上一点,
(x>0)上,过B作BC⊥x轴于点C,如图,P是y轴上一点,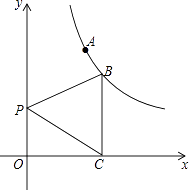
(1)求k的值及△PBC的面积;
(2)设点M(x1 , y1)、N(x2 , y2)(x2>x1>0)是双曲线y= ![]() (x>0)上的任意两点,s=
(x>0)上的任意两点,s= ![]() ,t=
,t= ![]() ,试判断s与t的大小关系,并说明理由.
,试判断s与t的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】送报员李师傅骑摩托车从报社出发,先向西行驶3千米到达A村,继续向西行驶2千米到达B村,然后向东行驶10千米到达C村,最后回到报社.
(1)若把李师傅的出发地记为0(即以报社为原点),以向东方向为正方向,在数轴上表示出A、B、C三个村庄的位置;
(2)A、C两个村庄相距多远?
(3)送报员李师傅一共骑行了多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
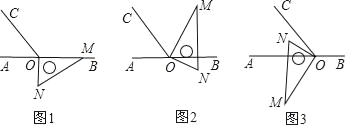
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=112°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,问:射线ON是否平分∠AOC?请说明理由;
(2)将图1中的三角板绕点O按每秒4°的速度沿逆时针方向旋转至图3,使射线ON恰好平分锐角∠AOC,求此时旋转一共用了多少时间?
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】假设我市出租车收费标准是:起步价6元,可乘3千米;3千米到5千米,每千米1.6元;超过5千米,每千米2.4元.
(1)若某人乘坐的路程为4千米,那么他支付的费用是多少?
(2)若某人乘坐了x(x>5)千米的路程,则他应支付的费用是多少?
(3)若某人乘坐的路程为10千米,那么他应支付的费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用图1,图2提供的某公司的一些信息,解答下列问题.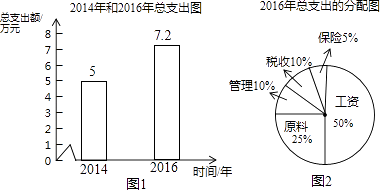
(1)2016年该公司工资支出的金额是万元;
(2)2014年到2016年该公司总支出的年平均增长率;
(3)若保持这种增长速度,请你预估该公司2017年的总支出.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在△ABC中,D是BC的中点,DE⊥BC,垂足为D,交AB于点E,且BE2-EA2=AC2,
(1)求证:∠A=90°.
(2)若DE=3,BD=4,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:(1)已知A(1,2),B(3,2),C(1,﹣1),D(﹣3,﹣3).在平面直角坐标系中描出这几个点,并分别找到线段AB和CD中点P1、P2,然后写出它们的坐标,则P1 ,P2 .
探究发现:(2)结合上述计算结果,你能发现若线段的两个端点的坐标分别为(x1,y1),(x2,y2),则线段的中点坐标为 .
拓展应用:(3)利用上述规律解决下列问题:已知三点E(﹣1,2),F(3,1),G(1,4),第四个点H(x,y)与点E、点F、点G中的一个点构成的线段的中点与另外两个端点构成的线段的中点重合,求点H的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com