
【题目】如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点A出发沿AD向点D匀速运动,速度是1cm/s;同时,点Q从点C出发沿CB方向,在射线CB上匀速运动,速度是2cm/s,过点P作PE∥AC交DC于点E,连接PQ、QE,PQ交AC于F.设运动时间为t(s)(0<t<8),解答下列问题: 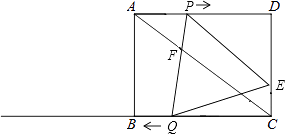
(1)当t为何值时,四边形PFCE是平行四边形;
(2)设△PQE的面积为s(cm2),求s与t之间的函数关系式;
(3)是否存在某一时刻t,使得△PQE的面积为矩形ABCD面积的 ![]() ;
;
(4)是否存在某一时刻t,使得点E在线段PQ的垂直平分线上.
【答案】
(1)
解:当PQ∥CD时,四边形PFCE是平行四边形,
此时,四边形PQCD是平行四边形,
则PD=CQ,即8﹣t=2t,
解得,t= ![]() ,
,
即当t= ![]() 时,四边形PFCE是平行四边形
时,四边形PFCE是平行四边形
(2)
解:∵PE∥AC,
∴△DPE∽△DAC,
∴ ![]() =
= ![]() =
= ![]() ,即
,即 ![]() =
= ![]() =
= ![]() ,
,
解得,DE=6﹣ ![]() t,PE=10﹣
t,PE=10﹣ ![]() t,
t,
则CE= ![]() t,
t,
∴y=S四边形PQCD﹣S△PDE﹣S△ECQ
= ![]() ×(8﹣t+2t)×6﹣
×(8﹣t+2t)×6﹣ ![]() ×(8﹣t+2t)×(6﹣
×(8﹣t+2t)×(6﹣ ![]() t)﹣
t)﹣ ![]() ×2t×
×2t× ![]() t
t
=﹣ ![]() t2+9t,
t2+9t,
即s与t之间的函数关系式为:y=﹣ ![]() t2+9t
t2+9t
(3)
解:矩形ABCD面积为:6×8=48,
由题意得,﹣ ![]() t2+9t=48×
t2+9t=48× ![]() ,
,
解得,t=2或6;
(4)
解:当点E在线段PQ的垂直平分线上时,EP=EQ,
由勾股定理得,(2t)2+( ![]() t)2=(8﹣t)2+(6﹣
t)2=(8﹣t)2+(6﹣ ![]() t)2,
t)2,
解得,t1= ![]() (舍去),t2=
(舍去),t2= ![]() ,
,
答:t= ![]() 时,点E在线段PQ的垂直平分线上
时,点E在线段PQ的垂直平分线上
【解析】(1)根据平行四边形的性质列出方程,解方程即可;(2)证明△DPE∽△DAC,根据相似三角形的性质用t表示出DE、CE、PE,根据面积公式计算即可;(3)根据题意列出一元二次方程,解方程即可;(4)根据线段垂直平分线的性质、勾股定理列式计算.


科目:初中数学 来源: 题型:
【题目】在如图所示的5×5的方格纸中,每个小正方形的边长为1,点A、B、C均为格点(格点是指每个小正方形的顶点).
(1)按下列要求画图:
①标出格点D,使CD∥AB,并画出线段CD;
②标出格点E,使CE⊥AB,并画出线段CE.
(2)CD与CE的关系是 .
(3)计算△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 两点,且点
两点,且点![]() 的横坐标为
的横坐标为![]() .
.

(1)求![]() 的值;
的值;
(2)若双曲线![]() 上一点
上一点![]() 的纵坐标为8,求
的纵坐标为8,求![]() 的面积;
的面积;
(3)过原点![]() 的另一条直线
的另一条直线![]() 交双曲线
交双曲线![]() 于
于![]() 两点(
两点(![]() 点在第一象限),若由点
点在第一象限),若由点![]() 为顶点组成的四边形面积为
为顶点组成的四边形面积为![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6cm,AD=4cm,点M是边AB的中点,点P是矩形边上的一个动点,点P从M出发在矩形的边上沿着逆时针方向运动,则当点P沿着矩形的边逆时针旋转一周时,△DMP面积刚好为5cm2的时刻有( ) 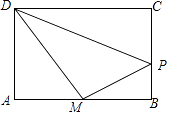
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
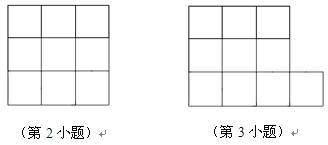
【题目】如图,有五个边长为1的小正方形组成的图形纸,我们可以把它剪开后拼成一个大正方形。

(1)拼成的大正方形的面积与边长分别是多少?
(2)你能在下图3×3方格中,连接四个格点,组成面积为5的正方形吗?
(3)你还能把十个小正方形组成的图形纸,剪开并拼成更大的正方形吗?若能,请在下图中画出图形,并求出它的边长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.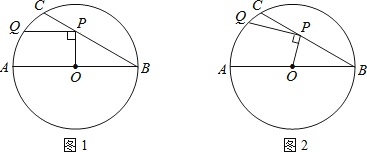
(1)如图1,当PQ∥AB时,求PQ的长度;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去年6月某日自治区部分市、县的最高气温(℃)如下表:
区县 | 吐鲁番 | 塔城 | 和田 | 伊宁 | 库尔勒 | 阿克苏 | 昌吉 | 呼图壁 | 鄯善 | 哈密 |
气温(℃) | 33 | 32 | 32 | 30 | 30 | 29 | 29 | 31 | 30 | 28 |
则这10个市、县该日最高气温的众数和中位数分别是( )
A.32,32
B.32,30
C.30,30
D.30,32
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com