
【题目】如图,已知直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 两点,且点
两点,且点![]() 的横坐标为
的横坐标为![]() .
.

(1)求![]() 的值;
的值;
(2)若双曲线![]() 上一点
上一点![]() 的纵坐标为8,求
的纵坐标为8,求![]() 的面积;
的面积;
(3)过原点![]() 的另一条直线
的另一条直线![]() 交双曲线
交双曲线![]() 于
于![]() 两点(
两点(![]() 点在第一象限),若由点
点在第一象限),若由点![]() 为顶点组成的四边形面积为
为顶点组成的四边形面积为![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)k=8;(2)15;(3) P坐标为(2,4)或(-2,-4)或(8,1)或(-8,-1).
【解析】
本题考查的是反比例函数的应用
(1)根据正比例函数先求出点A的坐标,从而求出了k值为8;
(2)根据k的几何意义,![]() ,
,![]() ;
;
(3)根据k的几何意义,![]() ,
,![]() .
.
(1)![]() 点
点![]() 横坐标为
横坐标为![]() ,
,![]() 当
当![]() 时,
时,![]() .
.![]() 点
点![]() 的坐标为
的坐标为![]() .
.
![]() 点
点![]() 是直线
是直线![]() 与双曲线
与双曲线![]() 的交点
的交点![]() .
.
(2)解法一:如图
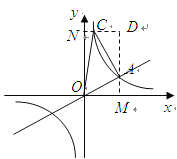
![]() 点
点![]() 在双曲线上,当
在双曲线上,当![]() 时,
时,![]()
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
过点![]() 分别做
分别做![]() 轴,
轴,![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,得矩形
,得矩形![]() .
.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() .
.
解法二:如图
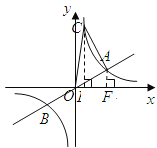
过点![]() 分别做
分别做![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,
,
![]() 点
点![]() 在双曲线
在双曲线![]() 上,当
上,当![]() 时,
时,![]() .
.
![]() 点
点![]() 的坐标为
的坐标为![]() .
.![]() 点
点![]() ,
,![]() 都在双曲线
都在双曲线![]() 上,
上,
![]()
![]() .
.
![]() .
.![]() ,
,![]() .
.
(3)![]() 反比例函数图象是关于原点
反比例函数图象是关于原点![]() 的中心对称图形,
的中心对称图形,
![]() ,
,![]() .
.![]() 四边形
四边形![]() 是平行四边形.
是平行四边形.
![]() .
.
设点![]() 横坐标为
横坐标为![]() ,得
,得![]() .
.
过点![]() 分别做
分别做![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,
,
![]() 点
点![]() 在双曲线上,
在双曲线上,![]() .
.
若![]() ,如图
,如图
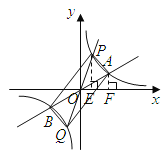
![]() ,
,
![]() .
.![]() .
.
解得![]() ,
,![]() (舍去).
(舍去).![]()
![]() .
.
若![]() ,如图
,如图
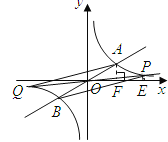
![]() ,
,
![]() .
.![]() ,
,
解得![]() ,
,![]() (舍去).
(舍去).![]() .
.
![]() 点
点![]() 的坐标是
的坐标是![]() 或
或![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图一,∠ACB=90°,点D在AC上,DE⊥AB垂足为E,交BC的延长线于F,DE=EB,EG=EB, 
(1)求证:AG=DF;
(2)过点G作GH⊥AD,垂足为H,与DE的延长线交于点M,如图二  找出图中与AB相等的线段,并证明.
找出图中与AB相等的线段,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级举行英语演讲比赛,购买A,B两种笔记本作为奖品,这两种笔记本的单价分别是12元和8元.根据比赛设奖情况,需购买笔记本共30本,并且所购买A笔记本的数量要不多于B笔记本数量的![]() ,但又不少于B笔记本数量
,但又不少于B笔记本数量![]() ,设买A笔记本n本,买两种笔记本的总费为w元.
,设买A笔记本n本,买两种笔记本的总费为w元.
(1)写出w(元)关于n(本)的函数关系式,并求出自变量n的取值范围;
(2)购买这两种笔记本各多少时,费用最少?最少的费用是多少元?
(3)商店为了促销,决定仅对A种类型的笔记本每本让利a元销售,B种类型笔记本售价不变.问购买这两种笔记本各多少本时花费最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
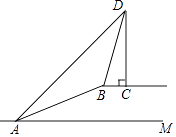
【题目】如图,斜坡AB的坡度为1:2.4,长度为26m,在坡顶B所在的平台上有一座电视塔CD,已知在A处测得塔顶D的仰角为45°,在B处测得塔顶D的仰角为73°,求电视塔CD的高度. (参考数值:sin73°≈ ![]() ,cos73°≈0.
,cos73°≈0. ![]() ,tan73°≈
,tan73°≈ ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为适应日益激烈的市场竞争要求,某工厂从2016年1月且开始限产,并对生产线进行为期5个月的升降改造,改造期间的月利润与时间成反比例;到5月底开始恢复全面生产后,工厂每月的利润都比前一个月增加10万元.设2016年1月为第1个月,第x个月的利润为y万元,其图象如图所示,试解决下列问题: 
(1)分别求该工厂对生产线进行升级改造前后,y与x之间的函数关系式;
(2)到第几个月时,该工厂月利润才能再次达到100万元?
(3)当月利润少于50万元时,为该工厂的资金紧张期,问该工厂资金紧张期共有几个月?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点A出发沿AD向点D匀速运动,速度是1cm/s;同时,点Q从点C出发沿CB方向,在射线CB上匀速运动,速度是2cm/s,过点P作PE∥AC交DC于点E,连接PQ、QE,PQ交AC于F.设运动时间为t(s)(0<t<8),解答下列问题: 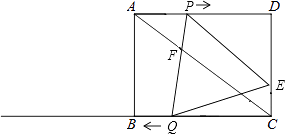
(1)当t为何值时,四边形PFCE是平行四边形;
(2)设△PQE的面积为s(cm2),求s与t之间的函数关系式;
(3)是否存在某一时刻t,使得△PQE的面积为矩形ABCD面积的 ![]() ;
;
(4)是否存在某一时刻t,使得点E在线段PQ的垂直平分线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列说法错误的是( )
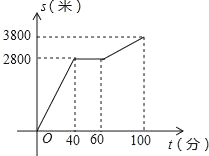
A. 小明中途休息用了20分钟
B. 小明休息前爬山的平均速度大于休息后爬山的平均速度
C. 小明在上述过程中所走的路程为6600米
D. 小明休息前爬山的平均速度为每分钟70米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,点E、F分别是AB、CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接AG、BG、CG、DG,且∠AGD=∠BGC.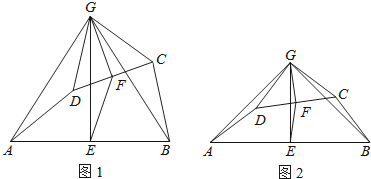
(1)求证:AD=BC;
(2)求证:△AGD∽△EGF;
(3)如图2 , 若AD、BC所在直线互相垂直,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
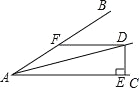
【题目】如图∠BAC=30°,D 为角平分线上一点,DE⊥AC 于 E,DF∥AC且交AB于F.
(1)求证:△ADF 是等腰三角形.
(2)若 DF=10cm,求 DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com